 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Законы булевой алгебры
Булева алгебра базируется на нескольких аксиомах.
Аксиомы операции отрицания:
Законы булевой алгебры вытекают из аксиом и имеют две формы выражения: для конъюнкции и дизъюнкции. Их правильность легко проверить по таблицам истинности либо путем подстановки 0 и 1 вместо соответствующих значений переменных.
Для примера преобразуем на основе законов булевой алгебры функцию
Раскроем скобки:. Так как Схемы, реализующие заданную функцию и полученную в результате преобразования, представлены на рис. 2.6, а, б.
Рис. 2.6. Схемы примера: а – по исходному уравнению (2.2); б – после преобразования
Аналогично можно минимизировать рассмотренное ранее выражение (2.1):
(закон дополнительности);
(закон универсального множества).
Схема, реализующая полученную функцию, представлена на рис. 2.7.
Рис. 2.7. Схема, полученная в результате минимизации уравнения (2.1)
Выражение (2.3) существенно проще, чем исходное уравнение (2.1). Построив для уравнения (2.3) таблицу истинности, можно убедиться, что она совпадает с данными табл. 2.3. В уравнении 2.3 некоторые конъюнкции, составляющие дизъюнкцию, содержат меньшее число аргументов, чем СДНФ. Выражение типа (2.3) называют дизъюнктивной нормальной формой или ДНФ. Совершенная дизъюнктивная форма является частным случаем ДНФ. После минимизации СДНФ число ДНФ и входящих в конъюнкции аргументов обычно меньше исходной СДНФ. Поэтому и схема, реализующая исходную функцию после минимизации, экономичнее построенной по СДНФ. Преобразование исходной логической функции выполняют с целью нахождения минимальной ДНФ. Специального правила, приводящего к минимальной ДНФ, не существует. Можно исследовать различные варианты и сравнить их результаты. Процедуру поиска облегчают специально разработанные методы минимизации, с которыми можно ознакомиться, например, по учебному пособию [7].
Поиск по сайту: |
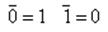













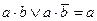




 , то
, то 



 (2.2)
(2.2) .
.
 . (2.3)
. (2.3) Для минимизации были использованы соотношения:
Для минимизации были использованы соотношения:
