 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ
Введение в алгебру логики
Алгебра логики – это формальный аппарат описания логической стороны процессов в цифровых устройствах. По имени автора этого математического аппарата Джорджа Буля его называют булевой алгеброй. Булева алгебра имеет дело с логическими переменными, которые могут принимать только 2 значения: истина и ложь, true и false, да и нет, 1 и 0. Наиболее распространено последнее обозначение. 1 и 0 – это не числа. Над ними нельзя производить арифметические действия. Эти логические переменные хорошо описывают состояния таких элементов, как реле, тумблеры, кнопки и т.п., т.е. таких элементов, которые могут находиться в двух состояниях: включено – выключено. К подобным объектам относятся и полупроводниковые логические элементы, на выходе которых может быть лишь один из двух уровней напряжения – низкий или высокий. Часто высокий = 1 (логич.), низкий = 0 (логич.). Функции алгебры логики принимают значения 1 или 0 в зависимости от значений аргументов. Одна из форм задания логической функции – табличная. Можно задавать логические функции словами или алгебраическими выражениями. Пример: компьютер следует приобрести, если есть в этом необходимость и имеются деньги. Набор трех логических функций НЕ, И, ИЛИ называют булевым базисом. Если Y – функция, а – аргумент, то можно рассматривать состояния
Таблица 2.1
Для 2 аргументов число комбинаций 4, для 3 – 23 = 8 и т. д. по степеням двойки. Булевый базис
Функция НЕ – это функция одного аргумента (отрицание, инверсия). Функция отрицания равна 1, когда ее аргумент равен 0, и наоборот. Отрицание отрицания аргумента равно самому аргументу: НЕ (НЕ ВКЛЮЧЕН) = ВКЛЮЧЕН. Электронный логический элемент, реализующий функцию НЕ в виде определенных уровней напряжения, называют инвертором.
Рис. 2.1. Условное графическое обозначение (а) и релейно-контактная реализация логического элемента НЕ (б) и (в)
На рис. 2.1 показано, что логическая функция НЕ может быть реализована различными способами включения контактных элементов. Функция И – это функция двух или большего числа аргументов (конъюнкция, логическое умножение). Обозначения: Y = a & b; Y = a ^ b; Y = a ∙b. Функция И равна 1 тогда и только тогда, когда все ее аргументы равны 1 (табл. 2.2). Союз И естественного языка, как правило, выражает именно это отношение. Например: лифт пойдет, если дверь закрыта И кнопка нажата. В релейно-контактной технике функция И реализуется последовательным включением замыкающих контактов (рис. 2.2). Только когда оба контакта замкнуты (а = 1 И в = 1), по цепи потечет ток и на нагрузке Rн создается падение напряжения URн. Элемент И часто используют для управления потоком информации. В этом случае на один его вход поступают информационные сигналы, а на другой – сигнал, разрешающий прохождение информации: 1 – пропускать, 0 – не пропускать. Такой элемент часто называют ключом (или вентилем).
Рис. 2.2. Таблица истинности, условное обозначение и релейно-контактная реализация логического элемента И
Условное изображение элемента И в схемах показано на рис. 2.2. Функция ИЛИ – это функция двух или большего числа аргументов (дизъюнкция). Функция ИЛИ равна 1, если хотя бы один из ее аргументов равен 1. В релейно-контактной технике функция ИЛИ реализуется параллельным включением замыкающих контактов (рис. 2.3). Обозначение функции ИЛИ: Y = a
Рис. 2.3. Таблица истинности, условное обозначение и релейно-контактная реализация логического элемента ИЛИ
На основе аналогии с релейно-контактными схемами или с помощью таблиц истинности для логического элемента И можно доказать следующие соотношения: а · 0 = 0; а · 1 = а; а · а = а; а · где а – аргумент, который может принимать значение 0 или 1. Для элемента ИЛИ аналогичное доказательство дает следующие соотношения: а
Поиск по сайту: |
 , то есть функция равна аргументу или
, то есть функция равна аргументу или 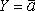 – это инверсия (рис. 2.1).
– это инверсия (рис. 2.1).

 b; Y = a + b. Последнее обозначение (знак +) применять не рекомендуется, поскольку в сложных случаях дизъюнкция (другое обозначение OR) будет смешиваться с двумя другими операциями: арифметическим суммированием и сложением по модулю 2.
b; Y = a + b. Последнее обозначение (знак +) применять не рекомендуется, поскольку в сложных случаях дизъюнкция (другое обозначение OR) будет смешиваться с двумя другими операциями: арифметическим суммированием и сложением по модулю 2.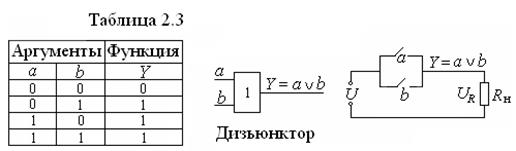
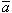 = 0,
= 0,