 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Арифметические операции над двоично-десятичными кодами чисел
При обработке больших массивов экономической информации переводы чисел из десятичной системы в двоичную и обратно могут требовать значительного машинного времени. Некоторые образцы ЭВМ поэтому имеют или встроенные, или подключаемые блоки, которые обрабатывают десятичные целые числа в их двоично-десятичном представлении. Действия над ними также приводятся к операции алгебраического сложения отдельных цифр чисел, представленных дополнительными кодами в соответствии с табл. 2.3. Приведем один из алгоритмов сложения, который получил довольно широкое распространение. 1. Сложение чисел начинается с младших цифр (тетрад) и производится с учетом возникающих переносов из младших разрядов в старшие. 2. Знак суммы формируется специальной логической схемой по знаку большего слагаемого. 3. Для того чтобы при сложении двоично-десятичных цифр возникали переносы, аналогичные при сложении чисел в десятичном представлении, необходимо проводить так называемую десятичную коррекцию. Для этого к каждой тетраде первого числа прибавляется дополнительно по цифре 610=01102, что позволяет исключить шесть неиспользуемых комбинаций (1010-1111)2, так как они кодируют шестнадцатеричные цифры A-F (числа 10-1510). 4. После операции суммирования осуществляется корректировка суммы. Из тех тетрад суммы, из которых не было переносов, изымаются ранее внесенные избытки 610=01102. Для этого проводится вторая коррекция. Операция вычитания заменяется, как и обычно, операцией сложения с числом -6,представленным дополнительным кодом 10102, но только в тех разрядах, в которых отсутствовали переносы. При этой второй коррекции переносы из тетрад блокируются. 5. Операция вычитания реализуется достаточно своеобразно. По общему правилу сложения (п.п.1-4) к тетрадам числа с большим модулем прибавляются дополнительные коды тетрад другого числа. В качестве знаке результата берется знак числа с большим модулем.
ОПЕРАТИВНЫЙ КОНТРОЛЬ ВЫЧИСЛИТЕЛЬНЫХ ОПЕРАЦИЙ ПО ВЫЧЕТАМ Расчетные соотношения
Контроль по вычетам (или по модулю) применяется для проверки правильности выполнения ряда вычислительных операций (арифметических, логических, операций пересылки данных, сдвига, преобразования в обратный или дополнительный код и др). В принципе любые данные, записанные в регистрах или ячейках памяти ЭВМ можно интерпретировать как некоторое целое число
где
При этом число A можно представить в виде:
где
Два целых числа
При этом предполагается, что вычеты чисел, записанных в регистрах (или в памяти), формируются без ошибок. При выполнении различных вычислительных операций над числами Рассмотрим некоторые свойства вычетов и операций сравнения. 1. 2. 3. 4. Если 5. Если 6. Из 7. Из сравнения 8. Если 9. Если 10. Если 11. Если Рассмотренные свойства часто применяются для проверки правильности выполнения различных вычислительных операций. В случае контроля с помощью встроенных аппаратных средств вместо числовых вычетов чаще используются цифровые вычеты (цифровой контроль по вычетам). При этом уменьшаются временные и аппаратные затраты. Цифровым вычетом числа
Отметим, что цифровой контроль, совпадающий с контролем по числовым вычетам возможно выполнять только в том случае, если
где Наиболее удобно выполнять цифровой контроль по модулям Решаемые задачи ориентированы на арифметические операции сложения и умножения, для которых справедливы приведенные выше свойства вычетов, и на логические операции «&», «Ú» и «исключающее или» (Å). При контроле арифметического деления используется косвенный метод контроля, так как в общем случае
Контроль арифметических операций Если 1. Вычисляются 2. Вычисляется 3. Вычисляется 4. Независимо вычисляется 5. Выполняется сравнение Если выполняется арифметическая операция умножения
Поиск по сайту: |

 , имеющее вид
, имеющее вид
 – разрядность кода;
– разрядность кода; - разрядные коэффициенты;
- разрядные коэффициенты; - вес i-го разряда (
- вес i-го разряда (  - основание кода);
- основание кода);
 ³ 2 – некоторый целый делитель числа
³ 2 – некоторый целый делитель числа  - целое частное (положительное или отрицательное);
- целое частное (положительное или отрицательное); 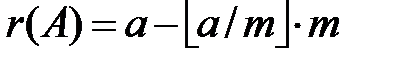 - остаток (всегда неотрицательный):
- остаток (всегда неотрицательный):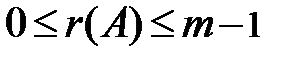
 носит название вычета или числового вычета числа
носит название вычета или числового вычета числа 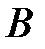 называются сравнимыми по модулю
называются сравнимыми по модулю 
 получится
получится 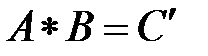 , где * - некоторая машинная операция. Над вычетами
, где * - некоторая машинная операция. Над вычетами 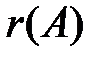 и
и  также выполняются соответствующие операции (может быть другие, но при отсутствии ошибок приводящие к результату, совпадающему с
также выполняются соответствующие операции (может быть другие, но при отсутствии ошибок приводящие к результату, совпадающему с  ). Считается, что если результат операции над остатками совпадает с
). Считается, что если результат операции над остатками совпадает с 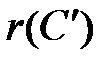 , то операция
, то операция 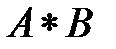 выполнена безошибочно. Отметим, что в большинстве случаев так оно и есть. Но, если
выполнена безошибочно. Отметим, что в большинстве случаев так оно и есть. Но, если 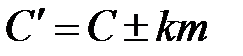 , то есть ошибка
, то есть ошибка  , то она будет замаскирована и результат сравнения приведет к неправильному заключению. При увеличении выбранного модуля
, то она будет замаскирована и результат сравнения приведет к неправильному заключению. При увеличении выбранного модуля 
 при любом целом
при любом целом 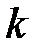 .
.
 , то
, то 
 (арифметическое умножение), то
(арифметическое умножение), то 
 и
и  следует
следует  и
и  .
. при любом целом
при любом целом  (обратное соотношение не всегда верно).
(обратное соотношение не всегда верно). то
то  при условии, что
при условии, что  при любом целом положительном
при любом целом положительном  , где
, где  - любое целое число, а
- любое целое число, а  (теорема Ферма).
(теорема Ферма). (следствие теоремы Ферма).
(следствие теоремы Ферма).
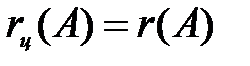 . Это равенство выполняется при выборе модуля
. Это равенство выполняется при выборе модуля  (8.1)
(8.1)
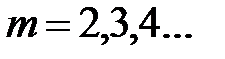 .
.
 (т.е.
(т.е.  . Например, для преобразования в восьмеричный код двоичные разряды объединяются в триады, для шестнадцатеричного кода выполняется объединение в тетрады и т.д., затем каждая группа представляется в соответствующем коде.
. Например, для преобразования в восьмеричный код двоичные разряды объединяются в триады, для шестнадцатеричного кода выполняется объединение в тетрады и т.д., затем каждая группа представляется в соответствующем коде.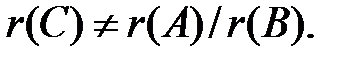 Рассмотрим основные этапы контроля по вычетам.
Рассмотрим основные этапы контроля по вычетам. , где
, где 
 , то выполняются следующие действия.
, то выполняются следующие действия. .
. (возможно с ошибкой)
(возможно с ошибкой) .
.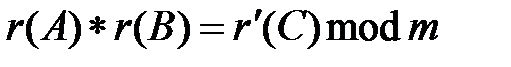 (штрих указывает на возможность ошибки).
(штрих указывает на возможность ошибки). и
и  . Если эти значения равны, то считается, что ошибка отсутствует, в противном случае вычисления повторяются.
. Если эти значения равны, то считается, что ошибка отсутствует, в противном случае вычисления повторяются.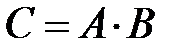 и результат округляется с обнулением
и результат округляется с обнулением  последних разрядов, то округленное число
последних разрядов, то округленное число 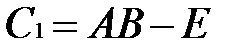 , где
, где  – число, записанное в
– число, записанное в  . При проверке находится реальное значение
. При проверке находится реальное значение  , затем остаток
, затем остаток 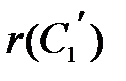 сравнивается с величиной
сравнивается с величиной  .
.