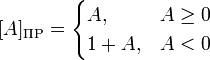Представление числа в прямом коде

При записи числа в прямом коде старший разряд является знаковым разрядом. Если его значение равно 0 — то число положительное, если 1 — то отрицательное. В остальных разрядах (которые называются цифровыми разрядами) записывается двоичное представление модуля числа.

Функция кодирования двоичных чисел (в том числе целых чисел и смешанных дробей) в прямом коде имеет вид:

где n — номер знакового разряда. В частности, при кодировании правильных двоичных дробей (то есть чисел − 1 < A < 1), n = 0 и функция кодирования принимает вид:

Величина числа A в прямом коде определяется по следующей формуле:

где:

§ a_sign — значение знакового разряда;

§ число A имеет k разрядов справа от запятой (дробная часть) и n разрядов слева (целая часть), тут учитываются только цифровые разряды.

Как видно из последней формулы, знаковый разряд в прямом коде не имеет разрядного веса. При выполнении арифметических операций это приводит к необходимости отдельной обработки знакового разряда в прямом коде.

Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения над натуральными числами. Ранее метод использовался в механических калькуляторах (арифмометрах). В настоящее время используется в основном в современных компьютерах.

Обратный n-разрядный двоичный код положительного целого числа состоит из одноразрядного кода знака (двоичной цифры 0), за которым следует n − 1-разрядное двоичное представление модуля числа (обратный код положительного числа совпадает с прямым кодом).

Пример. Двоичное представление числа 5 есть 101. Обратный 10-разрядный двоичный код числа +5 есть 0000000101.

Обратный n-разрядный двоичный код отрицательного целого числа состоит из одноразрядного кода знака (двоичной цифры 1), за которым следует n − 1-разрядное двоичное число, представляющее собой инвертированное n − 1-разрядное представление модуля числа.

Пример. Двоичное представление числа 5 есть 101, его 10-разрядное двоичное представление — 0000000101. Обратный 10-разрядный двоичный код числа −5 есть 1111111010.

Имеются два обратных кода числа 0: «положительный нуль» 0000000000 и «отрицательный нуль» 1111111111 (приведены 10-разрядные обратные коды).

n-разрядный обратный код позволяет представить числа от − 2^{n − 1} + 1 до + 2^{n − 1} − 1.

Двоичный пример

Метод дополнений в основном используется в двоичной системе счисления (с основанием 2₁₀), так как в двоичной системе счисления дополнение до 1 очень просто получается инверсией каждого бита (заменой '0' на '1' и наоборот) и добавлением единицы, дополнение до 2 может быть сделано симуляцией единицы переноса в младший значащий бит.^[1] Например:
вычитание 100₁₀ — 22₁₀

в методе дополнений становится суммой:

После отброса левой (старшей, начальной) «1» получается ответ: 01001110₂ (равное десятичным 78₁₀).

Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение). Либо вычитанием числа из нуля.

Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. ^[1]

Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2^N для N-битного дополнения до 2).

Поиск по сайту: