 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Матожидание распределения Пуассона ⇐ ПредыдущаяСтр 5 из 5
Дисперсия распределения Пуассона Пуассон Симеон Дени
1781-1840
Французский механик, физик, математик. Написал свыше 350 работ в области небесной механики, механики, определенных интегралов, дифференциальных урав-нений, рядов, теории вероятностей, статистики. Ввел термин «закон больших чисел» (1837 г.).
Геометрическое распределение Пусть проводится серия независимых испытаний; вероятность появления события А в каждом из них равна V Стрельба: до первого попадания, вероятность попадания равна 0.6. Найти вероятность того, что стрелок попадет с третьего раза. Ï Р(на 3 выстрел)=q* q*p=0.42·0.6=0.096 N Дискретная СВ имеет геометрическое распределение, если ее значения равны числу испытаний, которые надо провести до первого появления события А, а соответствующие вероятности равны Р(
Покажем, что
Матожидание и дисперсия геометрического распределения
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
Непрерывная СВ принимает все значения на каком-либо интервале. Типичный вид плотности и функции распределения для непрерывных СВ:
Дискретная СВ Непрерывная СВ (Число очков в секторе) (Расстояние до центра)
Вероятности Плотность распределения
Функция распределения
Непрерывной называют СВ, функцию распределения которой можно представить в виде
Функция
Свойства плотности распределения 1. 2. 3. 4. Вероятность того, что непрерывная СВ примет определённое значение, равна 0.
Не выясняют, примет ли непрерывная СВ определённое значение; всегда говорят о диапазоне значений.
Числовые характеристики непрерывных СВ. Матожидание непрерывной СВ М[Х]= М[х] существует, если Если все значения СВ принадлежат [a,b], то М[x]= Дисперсия непрерывной СВ D[Х]=M[(Х-M[Х])2]= Если все значения СВ принадлежат [a,b], то D[Х]= Все свойства матожидания и дисперсии те же , что и для дискретных СВ. D[Х]=s2[Х], s- среднеквадратическое отклонение.
Поиск по сайту: |
<
(без вывода).
. Испытания заканчиваются, как только событие А произошло. Т.е. если А появилось в к – ом испытании, значит, в первых к – 1 А не произошло.
=к)= 
.
.
= 
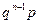
, где 
- сумма бесконечно убывающей геометрической прогрессии (откуда и название распределения). <
.
.
называется плотностью распределения, 
.
.
.
.
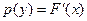сходится абсолютно.
