 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Представим неслучайную величину в виде
Тогда М[С]=С*р=С <
2. Постоянный множитель можно вынести за знак матожидания М [С Доказательство. Если СВ
тогда СВ С*
Найдем
3. Матожидание произведения двух независимых СВ равно произведению их матожиданий: М[XY]=М[X]М[Y]. Доказательство.
Следствие. Матожидание произведения нескольких взаимно независимых СВ равно произведению их матожиданий: М[X1…Xп]=М[X1]…М[Xп].
4. Матожидание суммы двух СВ равно сумме их матожиданий:: М[X+Y]=М[X]+M[Y]. Следствие. Матожидание суммы нескольких СВ равно сумме их матожиданий: М[X1+…+Xп]=М[X1]+…+М[Xп].
Дисперсия Зачастую важно знать, насколько далеко удаляются значения СВ от центра, т.е. как отклоняются значения СВ от своего матожидания.
Отклонением СВ называется разность между СВ и ее матожиданием : Х-М[Х]. СВ:
Отклонение
Свойство отклонения.Матожидание отклонения равно 0: М[Х-М[Х]]=0. Доказательство: М[Х-М[X]]=М[Х]-М[М[Х]]=М[Х]-М[Х]=0 < Почему? Одни отклонения положительные, другие – отрицательные. Для характеристики рассеянния отклонение не годится. Дисперсией СВ называется матожидание квадрата отклонения СВ от ее матожидания:
V. Найти дисперсию для СВ Х
Ï
Формула для вычисления дисперсии: D[X]=М[X2]-М2[х]: дисперсия равна разности между матожиданием квадрата СВ и квадратом ее матожидания. Доказательство: D[X]=М[(X-М[X])2]=М[X2-2X*М[х]+М2[х]]=М[х2]-М[2X*М[X]]+М[М2[X]]= =М[X2]-2М[X]М[X]+М2[X]=М[X2]-М2[X] <
Свойства дисперсии
1. Дисперсия постоянной величины равна 0: D[C]=0. (J какой разброс у константы?!)
2. Постоянный множитель выносится за знак дисперсии в квадрате:D[СХ]=С2D[Х]. Доказательство: D[СХ]=М[(СХ-М[СХ])2]=М[(СХ-СМ[Х])2]=М[С2(Х- М[Х])2]=С2D[Х] <
3. Дисперсия суммы нескольких взаимно независимых величин равна сумме их дисперсий: D[Х1+…Хп]=D[Х1]+…+D[Хп].
4. Дисперсия суммы СВ и постоянной величины равна дисперсии СВ: D[Х+С]=D[Х]. Доказательство: D[Х+С]=D[Х]+D[С]=D[Х] <
5. Дисперсия разности двух СВ равна сумме их дисперсий: D[Х-У]=D[Х]+D[У]. Доказательство: D[Х-У]=D[Х+(-1)У]=D[Х]+D[(-1)*У]+ D[Х]+ D[У] <
НЕКОТОРЫЕ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СВ
Поиск по сайту: |
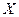

 ]=С*М [
]=С*М [  <
<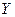
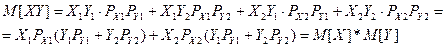 <
< .
.
 N
N