 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СВ
Рассмотрим характеристики, позволяющие количественно оценить СВ. Иногда этого достаточно. Самыми простыми являются среднее значение (центр тяжести СВ) и разброс значений СВ. Например - приложение к диплому. Средний балл показывает, кто лучше учится. Разброс – нестабильность.
Прежде чем давать определения таких характеристик, рассмотрим простейшие действия над случайными величинами.
Две СВ называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая СВ. В противном случае – зависимые. Несколько СВ называются взаимно независимыми, если законы распределения любого их числа не зависят от того, какие значения принимают остальные СВ.
Две дискретные СВ Х и Y называются независимыми, если для всех их возможных значений
Произведение независимых СВ Х и Y есть случайная величина Z=XY, возможные значения которой равны произведениям каждого значения СВ Х на каждое возможное значение СВ Y. Вероятности СВ Z равны произведению соответствующих вероятностей СВ Х и Y.
Сумма независимых СВ X и Y есть СВ Z=X+У , возможные значения которой равны суммам каждого возможного значение Х с каждым возможным значением Y. Вероятности значений Z равны произведению соответствующих вероятностей.
V Подбрасывание двух монет (одна обычная - Ï
Z=XY
Z=X+Y
N
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Математическим ожиданием дискретной СВ Матожидание – не случайная величина. Для каждой СВ матожидание определено однозначно и ничего случайного в нем нет. V Ï
Если СВ принимает счетное число значений, то матожидание СВ существует, если ряд V Найти матожидание появления события А в одном испытании, если Р (А) =р. ÏСВ Х - число появлений А в одном испытании
Cвойства математического ожидания 1. Матожидание постоянной величины равно ей: М[С]=С. Доказательство:
Поиск по сайту: |
 и
и  имеют место соотношения
имеют место соотношения .
.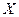
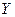

 называется сумма всех её возможных значений на их вероятности
называется сумма всех её возможных значений на их вероятности  .
. Найти
Найти 
 N
N сходится абсолютно.
сходится абсолютно.

 N
N