 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Прямий симплексний метод розвязку ЗЛП ⇐ ПредыдущаяСтр 5 из 5
Найбільш широко відомим числовим методом рішення задач лінійного програмування є симплексний метод або метод послідовного покращення плану. Для викладу симплексного методу припустимо, щоЗЛП представлена у вигляді:
Ввівши для задачі (33) позначення
Відносно отриманої задачі (34) зробимо наступні припущення: 1. rang 2. Задача (34) є невиродженою. Невиродженоюбудемо називати ЗЛП для якої всі її базисні плани невироджені. Невиродженим базисним планомназивається такий план, всі компоненти якого строго додатні. Зрозуміло, що для невиродженої задачі Запишемо матрицю умов задачі так де:
Відповідно Із області обмежень задачі (34) визначимо базисні змінні
Помножимо останню рівність на матрицю обернену до базисної
Звідси:
Також очевидно із (35), що базисний план для задачі (34) запишеться:
Підставимо отримане значення
Зрозуміло, що при початковому базисному плані (36) значення функції, яка оптимізується, буде рівним
Величини Покажемо, що якщо Дійсно Запишемо вектор
тоді
Співвідношення (39) справедливе, оскільки у цільову функцію доповнюючі змінні входять із нульовими коефіцієнтами, а при змінних
Відносно вектора оцінок 1. 2. Покажемо, що у першому випадку знайдено оптимальний базисний план ЗЛП, тобто задача розв’язана, а у другому випадку або лінійна форма ЗЛП необмежена на множині своїх планів, або можна перейти до наступного базисного плану, який покращить значення цільової функції задачі, що розглядається. У першому випадку цільову функцію збільшити неможливо за рахунок збільшення значення небазисних змінних, оскільки всі оцінки цих змінних додатні, а тому в (37) значення Нехай серед компонент вектора Однак
Можуть виникнути два випадки: 1. Покажемо, що в цьому випадку цільова функція буде необмеженою на множині своїх планів. Якщо 2.
З виразу (41)
Якщо б Елемент Переходом від одного базисного плану до іншого отримаємо послідовність базисів, а отже послідовність впорядкованих базисних розв’язків з монотонно зростаючим значенням цільової функції задачі (34). Оскільки число можливих базисів скінченне і ні один із базисів не може повторюватись, то за скінченне число кроків отримуємо розвязок задачі (34). З метою застосування прямого симплекс методу у практичних задачах опишемо його алгоритм. Нехай задана задача лінійного програмування:
Нехай rang 1. Будуємо початковий базисний план 2. Для кожного
3. Перевіряємо чи 4. Перевіряємо чи є в початковому базисному плані додатні значення 5. Знаходимо 6. Нехай 7. Нехай
Якщо мінімум досягається при 8. Здійснюємо перехід до нового базисного плану Стовбець вільних членів перераховуємо так:
Елементи матриці умов задачі знаходимо так:
Значення лінійної форми в новому базисі запишеться:
Елементи вектора оцінок шукаємо за формулами:
9. Переходимо до пункту 3 збільшивши індекс ітерації на 1. Кожен перехід до нового базису називається ітерацією симплексного методу. Описуючи теоретичні основи симплексного методу ми показали, що цей ітераційний процес є скінченним, а отже, за скінченне число кроків ми отримаємо розв’язок ЗЛП, або покажемо, що його не існує через необмеженість цільової функції або несумісність умов задачі При розв’язуванні ЗЛП на 1) Від задачі на 2) Розв’язувати ЗЛП на а) критерієм оптимальності плану при розв’язуванні задачі на б) за розв’язковий стовбець вибираємо той стовбець, якому відповідає максимальна додатня оцінка Приклад.Розв’яжемо з допомогою прямого алгоритму прямого симплекс-методу задачу лінійного програмування:
Запишемо цю задачу в канонічному вигляді, отримаємо:
Для цієї задачі початковий базисний план запишеться:
Застосуємо для ілюстрації симплек-методу табличний спосіб. Для кожної задачі, на кожну ітерацію складається нова симплекс-таблиця. Всі таблиці мають однакову структуру. Запишемо початкову симплекс-таблицю: Табл.2. Початкова симплекс таблиця для задачі (43).
Симплексна таблиця будується для ЗЛП в канонічній формі, вона включає стовбець базисних змінних, стовбець вільних членів, стовбець коефіцієнтів, з якими базисні змінні входять в цільову функцію, а також стовбці коефіцієнтів при всіх невідомих з області обмежень Для нашого прикладу 1). Прочитати базисний план, що відповідає даній симплекс-таблиці. Для цього базисним змінним надають значення із стовбця вільних членів, вільні змінні – рівні нулю. 2). Дати відповідь на запитання чи є даний базисний план оптимальним (проаналізувати чи серед оцінок В наведеному прикладі початковий базисний план (45) не є оптимальним, оскільки
Табл.3 Перша симплекс-таблиця для задачі (43).
Цій симплекс-таблиці відповідає план:
Оскільки в індексній стрічці є від’ємне значення, то це означає, що план (46) не оптимальний. Другий стовбець отриманої таблиці вибираємо за розв’язковий Табл.4. Друга симплекс-таблиця для задачі (43).
В індексній стрічці останньої симплекс-таблиці немає від’ємних оцінок. Це означає, що план
У зв’язку із цим симплекс-таблиця порахована не повністю. Максимальне значення цільової функції рівне [1] Номери введених в задачу доповнюючих та штучних змінних залежать від номерів обмежень до яких вони додаються. [2] У таблиці 2 елементи першого стовбця виділено
Поиск по сайту: |
 (33)
(33)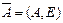 ,
, 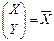 ,
,  приведемо її до вигляду:
приведемо її до вигляду: (34)
(34) ;
;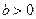 . З геометричної точки зору умова невироженості означає, що в ЗЛП відсутні вершини, в яких перетиналось би більше ніж
. З геометричної точки зору умова невироженості означає, що в ЗЛП відсутні вершини, в яких перетиналось би більше ніж  граничних гіперплощин (на площині прямих).
граничних гіперплощин (на площині прямих). ,
,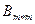 - базисна підматриця (із векторів при базисних змінних);
- базисна підматриця (із векторів при базисних змінних); - небазисна підматриця.
- небазисна підматриця. ,
,  .
. отримаємо
отримаємо
 , оскільки задача, що розглядається невироджена, то
, оскільки задача, що розглядається невироджена, то 
 (35)
(35) (36)
(36) (37)
(37)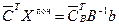 . Позначимо через
. Позначимо через  величину
величину  , де:
, де: -
-  -тий стовбець матриці умов
-тий стовбець матриці умов  ;
; - коефіцієнт при
- коефіцієнт при 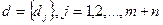 - вектором оцінок.
- вектором оцінок. – базисна змінна, тоді відповідне
– базисна змінна, тоді відповідне  . Для визначення оцінки скористаємося формулою
. Для визначення оцінки скористаємося формулою  ,
,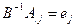 (
(  - вектор, у якого на місці
- вектор, у якого на місці  .
. у вигляді
у вигляді  , де
, де - відповідає змінним
- відповідає змінним  -мірний вектор);
-мірний вектор);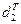 - відповідає змінним
- відповідає змінним  (
(  -мірний вектор).
-мірний вектор). (38)
(38) (39)
(39)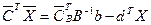 (40)
(40) ,
,  ,
, 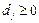 ;
; ,
,  .
. збільшити невдається.
збільшити невдається.
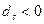 . Із виразу (40) видно, що в цьому випадку значення функції, що аналізується, можна збільшити на величину
. Із виразу (40) видно, що в цьому випадку значення функції, що аналізується, можна збільшити на величину  . Оскільки задача (34) на
. Оскільки задача (34) на  , то очевидно, що чим більше значення ми надамо величині
, то очевидно, що чим більше значення ми надамо величині  , тим на більшу величину зросте значення досліджуваної цільової функції ЗЛП.
, тим на більшу величину зросте значення досліджуваної цільової функції ЗЛП. , тобто найбільше значення, яке може мати змінна
, тобто найбільше значення, яке може мати змінна  (41)
(41) - вектор вільних членів в новому базисі;
- вектор вільних членів в новому базисі; - вектор коефіцієнтів при змінній
- вектор коефіцієнтів при змінній  .
. , то з виразу (41) видно, що
, то з виразу (41) видно, що  може приймати довільне додатнє значення, в тому числі
може приймати довільне додатнє значення, в тому числі 
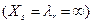 . Оскільки значення досліджуваної функції при переході до нового базису збільшується на величину
. Оскільки значення досліджуваної функції при переході до нового базису збільшується на величину  , то очевидно, що функція мети буде необмежена також.
, то очевидно, що функція мети буде необмежена також. .
. визначається лише одним способом, а саме
визначається лише одним способом, а саме (42)
(42) додатніх компонент, що суперечить припущенню про невиродженість. Якщо визначити з
додатніх компонент, що суперечить припущенню про невиродженість. Якщо визначити з  та в цільову функцію, отримаємо новий базисний план
та в цільову функцію, отримаємо новий базисний план  , який буде відрізнятися від попереднього базисного плану
, який буде відрізнятися від попереднього базисного плану  лише тим, що замість базисної змінної
лише тим, що замість базисної змінної  буде змінна
буде змінна  .
. 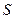 -товий стовбець, який вводиться в базис на текучій ітерації, називається розв’язковим. Індекс r, що задається співвідношенням (42) визначає розв’язковий рядок.
-товий стовбець, який вводиться в базис на текучій ітерації, називається розв’язковим. Індекс r, що задається співвідношенням (42) визначає розв’язковий рядок.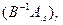 , що стоїть на перетині розв’язкового стовбця та розв’язкового рядка називається розв’язковим елементом.
, що стоїть на перетині розв’язкового стовбця та розв’язкового рядка називається розв’язковим елементом.
 . Наведемо кроки алгоритму
. Наведемо кроки алгоритму . Опишемо перехід від
. Опишемо перехід від  .
. ) обчислюємо оцінку:
) обчислюємо оцінку: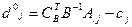 .
.
 . Якщо
. Якщо  , то
, то  – оптимальний базисний план.
– оптимальний базисний план.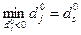 . Тоді
. Тоді  -товий стовбець буде розв’язковим стовбцем, а змінну
-товий стовбець буде розв’язковим стовбцем, а змінну  слід ввести в базу. Необхідно зауважити, що за розв’язковий стовбець можна вибрати будь-який стовбець, для якого
слід ввести в базу. Необхідно зауважити, що за розв’язковий стовбець можна вибрати будь-який стовбець, для якого  . Однак, зважаючи на те, що значення цільової функції змінюється на величину
. Однак, зважаючи на те, що значення цільової функції змінюється на величину 
 , де
, де  елементи розв’язкового стовбця. Якщо
елементи розв’язкового стовбця. Якщо  для
для  то лінійна форма вихідної задачі необмежена на множині планів, в протилежному випадку 7.
то лінійна форма вихідної задачі необмежена на множині планів, в протилежному випадку 7.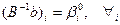
 .
. , то це означає що
, то це означає що  - розв’язковий елемент.
- розв’язковий елемент. вектором
вектором  у попередньому плані). Перехід до нового базису здійснюємо при допомозі формул:
у попередньому плані). Перехід до нового базису здійснюємо при допомозі формул:


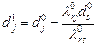
 можна:
можна: ,
, 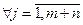 ;
;
 ,
, 
 (43)
(43)
 (44)
(44) ;
;  . (45)
. (45)









 ,
,  , тому
, тому  , а саме
, а саме  . Кожен студент повинен вміти прочитати та проаналізувати симплекс-таблицю, а саме:
. Кожен студент повинен вміти прочитати та проаналізувати симплекс-таблицю, а саме: виконується
виконується  ).
). . Тому вибираємо перший стовбець за розв’язковий[2], тобто змінну
. Тому вибираємо перший стовбець за розв’язковий[2], тобто змінну  , це означає, що змінну
, це означає, що змінну  досягається для першого рядка). Таким чином розвязковий елемент
досягається для першого рядка). Таким чином розвязковий елемент 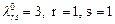 . Здійснивши симплекс перетворення, за формулами кроку 8 алгоритму, відносно розвязкового елемента, отримаємо наступну симплекс таблицю.
. Здійснивши симплекс перетворення, за формулами кроку 8 алгоритму, відносно розвязкового елемента, отримаємо наступну симплекс таблицю.



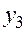
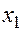
 ,
,  . (46)
. (46)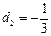 , тобто змінну
, тобто змінну  , тобто змінну
, тобто змінну  виводимо з числа базисних. Значення розв’язкового елемента
виводимо з числа базисних. Значення розв’язкового елемента  . В результаті симплексного перетворення відносно розв’язкового елемента отримаємо другу симплексну таблицю.
. В результаті симплексного перетворення відносно розв’язкового елемента отримаємо другу симплексну таблицю.







 оптимальний:
оптимальний: .
. .
.