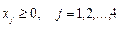Постановка задачі лінійного програмування

Лінійне програмування

В найзагальнішому виді задача лінійного програмування формулюється так:

треба знайти значення n змінних x₁,x₂,…,x_n, які задовільняють системі співвідношень типу:

(2)

(3)

і при цьому визначають найбільше (найменше) значення функції

(1)

Тут a_ij, b_i, c_j - задані дійсні числа. Крім того, в кожному із співвідношень (2) може використовуватись лише один із знаків ≤, =, ≥ , хоч різні співвідношення можуть мати різні знаки.

Співвідношення (умови) (2), (3) називаються обмеженнями, а функція (1) - цільовою функцією задачі. Суттєвим є те, що ліві частини всіх обмежень (2) - (3) і функція (1) є лінійними відносно змінних x₁,x₂,…,x_n. Якраз через це задачу (1)-(3) називають задачею лінійного програмування (ЗЛП).

Будь-який впорядкований набір (вектор) (x₁⁰,x₂⁰,…,x_n⁰)значень змінних, який задовільняє всім обмеженням (2)-(3) (тобто, будь-який розв‘язок системи лінійних рівнянь і нерівностей (2)-(3)), називається допустимим розв'язком або планом задачі.

Допустимий розв‘язок задачі лінійного програмування, який оптимізує (максимізує або мінімізує) її цільову функцію, називається оптимальним розв'язком (оптимальним планом) задачі.

Приклад: Нехай дана задача лінійного програмування:

знайти максимум функції L = -8 x₁+x₂+4x₃ - x₄

при обмеженнях:

2 x₁+x₂ - x₃+x₄≤8

- x₁+x₂+8x₃ - 2x₄≥6

x₁ -2x₂+3x₃ - x₄=2

Легко перевірити, що такі, наприклад, набори x₁=1, x₂=1, x₃=1, x₄=0 та x₁=0, x₂=2, x₃=2, x₄=0 значень невідомих є допустимими розв'язками даної задачі, тому що задовільняють обмеження. А, наприклад, набір x₁=1, x₂=0, x₃=2, x₄=-1 не є допустимим розв'язком задачі, оскільки не задовільняються третє обмеження і обмеження на знак змінної х₄.

Знайдемо значення цільової функції для відповідних допустимих розв'язків.

Для першого маємо:

L=-8*1+1*1+4*1-1*0= -3

для другого:

L=-8*0+1*2+4*2-1*0= 10

Оскільки значення цільової функції для першого допустимого розв'язку є менше, ніж значення цільової функції для другого допустимого розв'язку, то зрозуміло, що перший допустимий розв'язок не є оптимальним розв'язком даної задачі. Що стосується другого допустимого розв'язку, то без додаткового дослідження не можна сказати чи є він оптимальним розв'язком задачі, чи ні.

Зрозуміло, що не кожна задача лінійного програмування має допустимий розв'язок, тому що не кожна система рівнянь і нерівностей має розв'язок. Задачу, яка не має жодного допустимого розв'язку, будемо називати нерозрішимою через несумісність умов.

Виявляється теж, що не для всякої задачі, яка має допустимі розв'язки, існує оптимальний розв'язок. Такі задачі будемо називати нерозрішимими через необмеженість цільової функції.

Поиск по сайту: