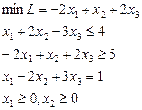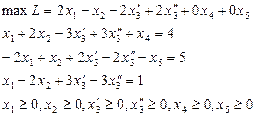|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Канонічна форма задачі лінійного програмування
Розглядаючи різні практичні задачі з лінійними обмеженнями і лінійною цільовою функцією бачимо, що в одних задачах обмеження мають вигляд нерівностей типу ≤, в інших ≥, в третіх - типу =. В одних задачах треба знайти максимум цільової функції, в інших - мінімум. Не у всіх задачах вимагається невідємність змінних. Така різноманітність форм запису задач лінійного програмування ускладнює дослідження загальних властивостей задач і вимагає розробки спеціальних методів для розвязування кожного з можливих типів задач. У звязку з цим домовились кожен з типів зводити до єдиної форми , яку назвали канонічна форма.Ця форма проста і зручна для дослідження. Вважатимемо, що ЗЛП записана у канонічній формі, якщо вона формулюється наступним чином: max
Введемо позначення:
За таких позначень канонічна форма задачі набуде вигляду:
або, використавши введені вище позначення, отримаємо компактний запис ЗЛП:
Це матрична форма запису канонічної задачі лінійного програмування (матриця А називається матрицею умов задачі). Ми будемо також використовувати так звану векторну форму запису канонічної задачі лінійного програмування, тому для стовпців матриці А введемо позначення:
Тоді задачу лінійного програмування можна записати так:
Це векторна форма запису канонічної задачі лінійного програмування. Разом з тим для деяких практичних, і теоретичних цілей застосовується і так звана симетрична форма запису задачі лінійного програмування, яка має вигляд:
Покажемо, як будь-яку задачу лінійного програмування звести до канонічного виду. Нехай задача лінійного програмування має вигляд:
Введемо
Віднявши від лівих частин обмежень (6) додаткові невід'ємні змінні
Додаткові змінні
Між задачею (4)-(7) і задачею (8)-(11) є тісний зв'язок, а саме: кожному допустимому розв’язку
а для обмежень (10) справедливо:
Справедливим є і обернене твердження: кожному допустимому розв'язку Додаткові змінні Приклад. Звести до канонічного виду задачу:
Вводимо додаткові змінні
Якщо вихідна задача лінійного програмування є задачею мінімізації, то для зведення до канонічного виду така задача замінюється еквівалентною їй задачею максимізації. Легко переконатись; що мінімум функції
При цьому Таким чином, якщо треба звести до канонічного виду задачу мінімізації цільової функції Щоб отримати оптимальне значення вихідної задачі, треба взяти оптимальне значення перетвореної задачі із оберненим знаком. Якщо у вихідній задачі не на всі змінні накладається умова невід'ємності, то і при виконанні розглянутих вимог така задача ще не буде задачею канонічного виду. Для того, щоб представити таку задачу у канонічному виді, кожну із змінних
Підставивши різниці типу (12) у вихідну задачу, отримуємо еквівалентну їй задачу (канонічну, якщо інші вимоги щодо канонічного виду задовольняються). Приклад. Звести до канонічного виду задачу лінійного програмування:
Відповідь:
Поиск по сайту: |

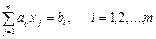
 .
. ,
,  ,
,  ,
,
 ,
, ,
, ,
, 

 ,
, 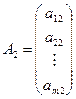 ,...,
,..., 


 (4)
(4) (5)
(5)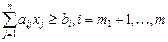 (6)
(6) (7)
(7) додаткових невід'ємних змінних
додаткових невід'ємних змінних 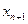 ,
,  ,…,
,…,  .Для того, щоб нерівності (5) перетворити в рівності, до їх лівих частин додамо додаткові змінні
.Для того, щоб нерівності (5) перетворити в рівності, до їх лівих частин додамо додаткові змінні  .Після цього система нерівностей (5) набуде вигляду:
.Після цього система нерівностей (5) набуде вигляду:
 ,…,
,…, 
 в цільову функцію введемо з коефіцієнтами, рівними нулеві. Отримаємо задачу:
в цільову функцію введемо з коефіцієнтами, рівними нулеві. Отримаємо задачу: (8)
(8) (10)
(10) (11)
(11) задачі (4)-(7) відповідає повністю визначений розв'язок
задачі (4)-(7) відповідає повністю визначений розв'язок  задачі (8)-(11), де для обмежень (9) виконується
задачі (8)-(11), де для обмежень (9) виконується
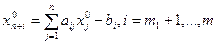
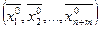 задачі (8)-(11) відповідає повністю визначений допустимий розв’язок
задачі (8)-(11) відповідає повністю визначений допустимий розв’язок  і їх відкидання в лівих частинах рівностей (9) і (10) робить твердження очевидним).
і їх відкидання в лівих частинах рівностей (9) і (10) робить твердження очевидним). входять в цільову функцію (8) з нульовими коефіцієнтами, тому значення цільових функцій (4) і (8) для відповідних допустимих розв'язків є однаковими. Якщо одна із задач не має оптимального розв’язку, то й інша також його не має.
входять в цільову функцію (8) з нульовими коефіцієнтами, тому значення цільових функцій (4) і (8) для відповідних допустимих розв'язків є однаковими. Якщо одна із задач не має оптимального розв’язку, то й інша також його не має.
 ,
, 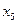 змінну
змінну 
 із якими-небудь обмеженнями на змінні (чи без них) є рівним максимуму функції
із якими-небудь обмеженнями на змінні (чи без них) є рівним максимуму функції  , взятому з протилежним знаком, тобто
, взятому з протилежним знаком, тобто
 і
і  досягаються при одних і тих же значеннях змінних. Тут має місце повна аналогія з випадком функції однієї змінної, коли твердження є очевидним.
досягаються при одних і тих же значеннях змінних. Тут має місце повна аналогія з випадком функції однієї змінної, коли твердження є очевидним. то досить замість даної функції взяти за цільову функцію
то досить замість даної функції взяти за цільову функцію  (тобто змінити знаки при коефіцієнтах цільової функції L на протилежні).
(тобто змінити знаки при коефіцієнтах цільової функції L на протилежні). , на яку не накладено умову невід’ємності, замінюють різницею двох невід’ємних змінних:
, на яку не накладено умову невід’ємності, замінюють різницею двох невід’ємних змінних: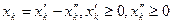 (12)
(12)