Приклади економічних задач лінійного програмування

Задача про найкраще використання ресурсів.

Нехай деяке підприємство має в своєму розпорядженні ресурси різних видів - сировину, робочу силу, обладнання тощо (і=1,2,...,т - індекс виду ресурсу). Кількості ресурсів відповідно рівні b_i - (і=1,2,...,т). На основі цих ресурсів можна випускати п видів продукції (j=1,2,...,n - індекс виду продукції). Прибуток від реалізації одиниці продукції j-гo виду дорівнює p_j (j=1,2,...,n). Відомі також необхідні кількості витрат і-го ресурсу на виробництво одиниці продукції j-гo виду - a_ij.Необхідно визначити такі обсяги випуску продукції кожного виду x_j (j=1,2,...,n), які б забезпечували отримання максимального прибутку при заданих обмеженнях на використовувані ресурси.

Введені позначення дозволяють побудувати математичну модель даної задачі. Оскільки p_j прибуток від реалізації одиниці продукції j-говиду, то x_j одиниць забезпечують p_jx_j одиниць прибутку. Загальний прибуток (позначимо його через Р) буде рівним Р=р₁х₁ + р₂х₂+…+р_пх_п

Отриманий вираз є цільовою функцією задачі.

Сформулюємо систему обмежень. Очевидно a_ijх_j - витрати і-го ресурсу на виробництво х_j одиниць продукції j-говиду. Підсумувавши витрату і-го ресурсу на випуск всіх видів продукції, отримаємо загальну витрату цього ресурсу. Вона не повинна перевищувати об‘єму b_i (і=1,2,...,т), тобто

а₁₁х₁+ а₁₂х₂+…+ а_1пх_п ≤ b₁

а₂₁х₁+ а₂₂х₂+…+ а_2пх_п ≤ b₂

………………………………

а_т1х₁+ а_т2х₂+…+ а_тпх_п ≤ b_m .

Щоб шуканий план виробництва був реальним, необхідно вказати, що обсяги випуску продукції кожного виду повинні бути невід‘ємні, тобто

Таким чином задача про найкраще використання ресурсів в компактному записі матиме вигляд:

,

і є, очевидно, типовою задачею лінійного програмування.

Приклад: Для виготовлення двох видів продукції П₁ і П₂ використовують три види сировини С₁, С₂, С₃. Запаси сировини, кількість одиниць сировини, які витрачаються на виготовлення одиниці продукції кожного виду, а також величина прибутку від реалізації одиниці продукції, наведені в таблиці:

Табл.1. Вихідні умови задачі.

Позначимо через х₁ кількість одиниць продукції П₁ а через х₂ - кількість одиниць продукції П_2, яку ми будемо виготовляти. Тоді, враховуючи кількість одиниць сировини, які витрачаються на виробництво одиниці продукції кожного виду, а також запаси сировини, отримаємо систему обмежень:

х₁+ 5х₂ ≤ 15

4х₁+ 5х₂ ≤ 20

10х₁+ 2х₂ ≤ 35

x₁ ≥0, x₂ ≥0,

яка показує, що кількість сировини, яка витрачається на виготовлення продукції, не може перевищити наявних запасів, а також те, що випуск продукції не може бути від‘ємною величиною.

Кінцеву ціль задачі - отримання максимального прибутку від реалізації (а ми приймаємо , що вся випущена продукція реалізується) - виразимо як функцію двох змінних х₁ і х₂. Реалізація х₁ одиниць продукції дає прибуток 20х₁ грн., х₂ одиниць продукції П₂ - прибуток 10х₂ а, отже, сумарний прибуток Р буде рівний 20х₁ + 10х₂. Тоді задача оптимального використання сировини полягатиме у відшуканні таких невід‘ємних значень х₁ і х₂ при яких прибуток Р буде максимальним за умови не перевищення витрат сировини (ресурсів) над їх запасами:

max P = 20х₁ + 10х₂

х₁+ 5х₂ ≤ 15

4х₁+ 5х₂ ≤ 20

10х₁+ 2х₂ ≤ 35

x₁ ≥0, x₂ ≥0.

Поиск по сайту:
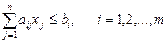
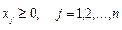