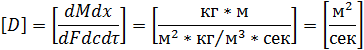Диффузионное подобие. Критериальное уравнение конвективного массообмена

Перенос вещества между фазами осуществляется одновременно молекулярной и конвективной диффузией. В массе фазы, вследствие интенсивного перемешивания концентрация распределяемого вещества в каждом сечении системы почти одинакова, и поэтому перенос вещества осуществляется преимущественно конвективной диффузией, т.е. движущимися частицами носителя и распределяемого вещества.

В пограничном слое перенос вещества осуществляется как молекулярной, так и конвективной диффузией. У поверхности раздела фаз возрастает роль молекулярной диффузии. Если массообмен происходит между твёрдой фазой и жидкостью или газом, то внутри твёрдой фазы перенос вещества осуществляется массопроводностью. Закон массопроводности аналогичен закону молекулярной диффузии.

Перенос вещества молекулярной диффузией определяется первым законом Фика, согласно которому количество продиффундировавшего через слой вещества пропорционально градиенту концентрации, времени и поверхности слоя, перпендикулярной к направлению диффузионного потока,

dM = -D × dc/dx ×dFdt,

где М – количество продиффундировавшего вещества, кг (кгс).

dc/dx - градиент концентрации в направлении диффузии, (кг/м3)/м.

F – площадь слоя, через который происходит диффузия вещества, м2.

t - время, сек (ч); D – коэффициент диффузии.

Коэффициент диффузии зависит от свойств диффундирующего вещества и среды, в которой происходит диффузия, а также от температуры и давления.

Размерность D определяется из уравнения Фика.

При конвективной диффузии перенос вещества осуществляется движущимися частицами носителя и распределяемого вещества.

При конвективной диффузии количество переносимого вещества из фазы, отдающей вещество, к поверхности раздела фаз пропорционально поверхности фазового контакта, времени, частной движущей силе, т.е. разности концентрации распределяемого вещества в фазе и у поверхности раздела.

dM = b×dF×dt×Dc, [кг/кмоль] (1)

где F – поверхность фазового контакта, м2.

t - время, сек.

Dc – частная движущая сила процесса.

b - коэффициент массопередачи.

В СИ:

Дифференциальное уравнение переноса массы в движущемся потоке.

Это уравнение дополняется граничными условиями диффузии. Количество вещества, перемещающегося из фазы к границе раздела фаз, определяется уравнением конвективной диффузии: dM = b×dF×dt×Dc (1)

У поверхности раздела фаз это же количество вещества перемещается в другую фазу за счёт молекулярной диффузии и определяется по уравнению молекулярной диффузии.

dM = -D×dc/dx ×dF×dt (2)

После сравнения уравнений (1) и (2) получим

bDc = -D×dc/dx - математическую формулировку граничных условий.

Полученные дифференциальные уравнения конвективного массообмена аналитически неразрешимы, поэтому методом теории подобия из них получают критериальные уравнения для определения коэффициента массоотдачи.

Методом теории подобия из уравнения граничных условий выводится безразмерный критерий подобия

b×l/D = idem – характеризующий обмен веществ на границе фаз: по своей структуре совершенно аналогичен критерию Нуссельта.

Nu’ = b×l/D, где l – характерный линейный размер, м. (сравнить с Nu = a×l/l)

Другой критерий подобия диффузионных процессов получается путём преобразования дифференциального уравнения конвективного массообмена. Упрощённо напишем только относительно оси х.

- из этого уравнения получается безразмерный комплекс

w×l/D = idem

Pe’ = w×l/D - диффузионный критерий Пекле.

При вынужденном движении потока конвективный массообмен можно представить в виде функции от критериев подобия:

f(Pe’, Nu’, Re, Г) = 0,

где Г - симплекс геометрического подобия, выражающий отношения различных

геометрических размеров аппаратов Г = l1/lo (l1 и lo – величины,

характеризующие размеры стенок)

Коэффициент массоотдачи является неопределяющим параметром. Поэтому критерий Нуссельта можно представить в виде функциональной зависимости от определяющих критериев:

Nu’ = A×Rem×Pr’n×Гk

причём A, m, n, k – находят опытным путём.

Поиск по сайту: