 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Ламинарное движение жидкости. Cредняя скорость потока при ламинарном движении
При относительно небольших скоростях жидкость движется параллельными струйками, не смешивающимися друг с другом. Такое движение жидкости называют струйчатым или ламинарным. Струйки обладают различными скоростями: в слое, непосредственно соприкасающемся со стенками, вследствие прилипания скорость равняется нулю и достигает максимального значения в слое, движущемся по оси трубы. Рассмотрим распределение скоростей и расход жидкости при установившемся ламинарном потоке. Вследствие действия между слоями сил трения слои будут двигаться с неодинаковыми скоростями. Центральный цилиндрический слой у оси трубы имеет максимальную cкорость, по мере удаления от оси, скорость элементарных кольцевых слоёв будет уменьшаться. Непосредственно у стенки скорость жидкости равна нулю
Выделим в потоке жидкости, ламинарно движущейся по трубе с радиусом R, цилиндрический слой l и радиусом r.
Движению цилиндра оказывает сопротивление сила внутреннего трения, согласно закону Ньютона равна. где Wr – скорость движения жидкости вдоль оси цилиндра на расстоянии r от оси; F = 2prl – наружная поверхность цилиндра; m - вязкость жидкости. В соответствии с законами динамики для установившегося движения можно написать уравнение : После подстановки и сокращения переменных, получим выражение для При r = R, W = 0, а при r = 0, Wr = Wmax уравнение
Откуда Wr можно выразить через Wmax: Уравнение представляет собой закон Стокса, выражающий параболическое распределение скоростей в сечении трубопровода при ламинарном движении. Согласно этому закону скорость течения жидкости у стенки трубы равна нулю и максимальна по оси трубы. Средняя скорость равна половине максимальной Для определения расхода жидкости при ламинарном движении рассмотрим элементарное кольцевое сечение с внутренним радиусом r и внешним радиусом (r + dr), площадь которого равна dS = 2prdr. Умножая скорость слоя жидкости на площадь его сечения, получим расход жидкости: dVсек = 2prdrWr, интегрируя выражение найдём расход жидкости для всей площади сечения трубы. Интегрируя от r = 0 до R получим Подставив вместо Wr его значение из выражения и разделив расход жидкости на площадь сечения трубы найдём среднюю скорость:
Сопоставляя значение Wср со значением Wмакс, находим, что Wср равна половине Wмакс.
Поиск по сайту: |
 .
.

 Движение слоя происходит под действием сил давления P1 и P2 с обеих торцевых сторон цилиндра: , где P1 и P2 - гидростатическое давление в сечениях 1-1 и 2-2.
Движение слоя происходит под действием сил давления P1 и P2 с обеих торцевых сторон цилиндра: , где P1 и P2 - гидростатическое давление в сечениях 1-1 и 2-2.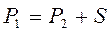 .
.




