|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение достоверности отличия нескольких наборов частот ⇐ ПредыдущаяСтр 6 из 6
Более частым случаем использования критерия является сравнение наскольких наборов частот. Технология расчета здесь похожа. Для исходной таблицы размером n на k с исходными количествами Nij рассчитываются ожидаемые количества Mij, которые были бы, если бы частоты в каждом столбце были бы одинаковыми. После чего вычисляется различие
Для этого можно сравнивать группы попарно и рассчитывать достоверность различий в каждой паре. Кроме того, тут решается еще одна техническая проблема. Однако для таблиц 2 на 2 есть точное решение Фишера, для которого вне зависимости от объема наблюдений достоверность различия рассчитывается правильно[3]. Поэтому есть возможность, переходя к таблицам 2 на 2, получить точное значение р. Для расчета попарных достоверностей различия частот, относительных рисков и границ к относительным рискам удобно воспользоваться программой, выложенной на проект 1mgmu.com. После загрузки главной страницы нужно перейти по ссылке «Программа определения достоверности различий частот точным тестом Хи-квадрат». Рассмотрим пример. Пусть среди лиц с инфекционным вирусным гепатитом мы определяем 5-летнюю выживаемость и получили следующие данные:
Рассчитаем общее количество и количество умерших, вычитая количество умерших их общего количества:
Получим:
Рассчитаем летальность
Получим:
Рассчитаем ожидаемое количество умерших, умножив фактическое количество больных на общую летальность (заодно вставив первую строку для подзаголовков):
Ожидаемое количество выживших получим, вычитая из общего количества больных ожидаемое количество умерших:
Рассчитаем различие между ожидаемым и фактическим количеством:
Размножим рассчитанные различия:
Просуммируем суммарное различие. При этом суммируются все 6 ячеек с различиями:
Рассчитываем достоверность различий при помощи функции ХИ2РАСП. Так как анализируемая таблица 3 на 2, то число степеней свободы – 2:
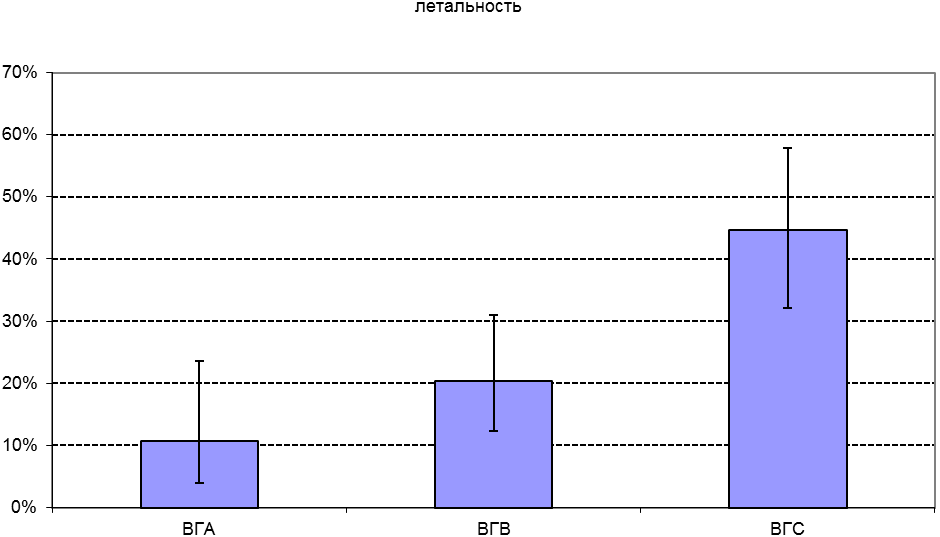
Полученное р – около 0,002, то есть высокодостоверно. Строим график.
При помощи программы расчета доверительной вероятности определяем доверительные границы к летальности. При этом в качестве числа наблюдений надо брать общее число больных, а в качестве «успешных наблюдений» - число летальных исходов. Например, для первой строки с ВГА число наблюдений будет 28, а число успехов – 3.
Добавляем погрешности на график:
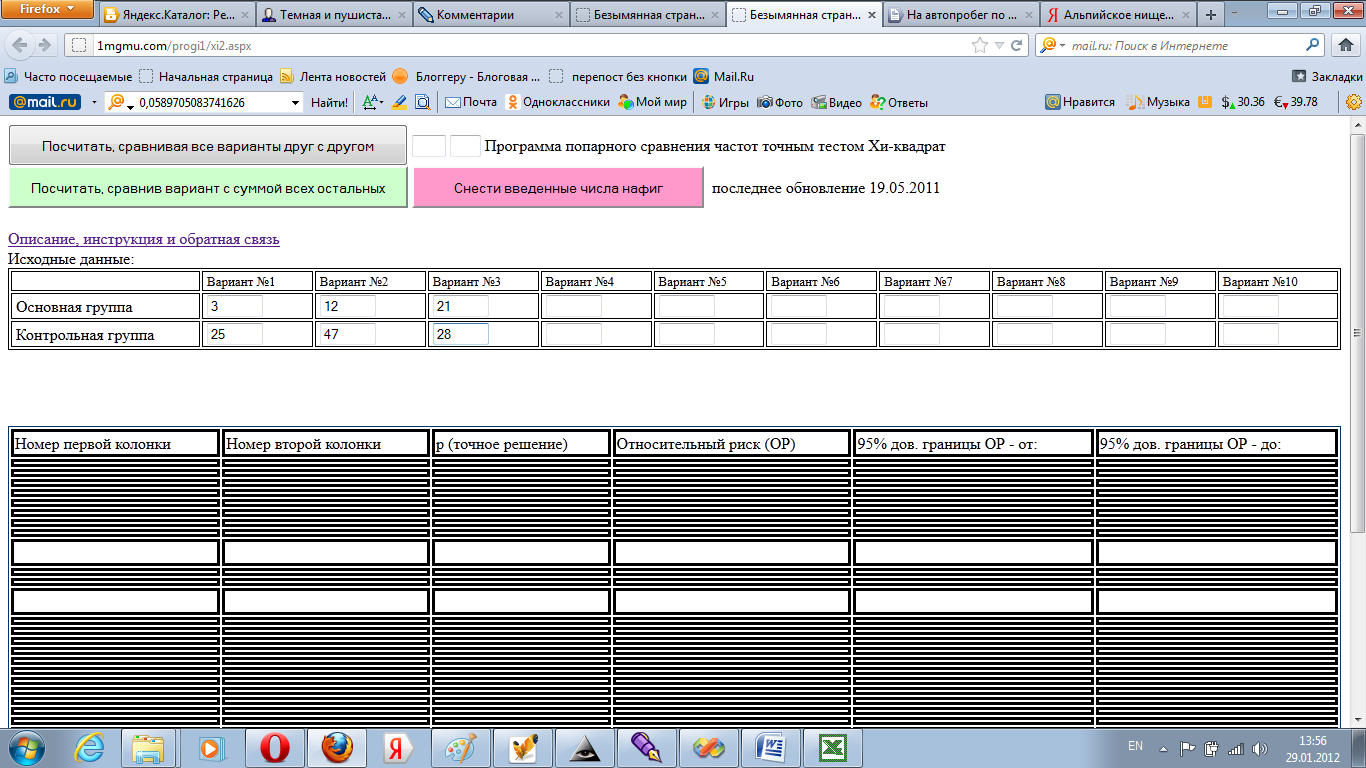
Из графика видно, что летальность у больных ВГА и ВГВ достоверно не различается, а у ВГС – выше. Однако желательно пересчитать поточнее, особенно если учесть, что у ВГА ожидаемое число умерших лишь немного больше 5. Обращаемся к программе «Программа определения достоверности различий частот точным тестом Хи-квадрат» на том же проекте Для рассмотренного варианта исходные данные надо внести следующим образом:
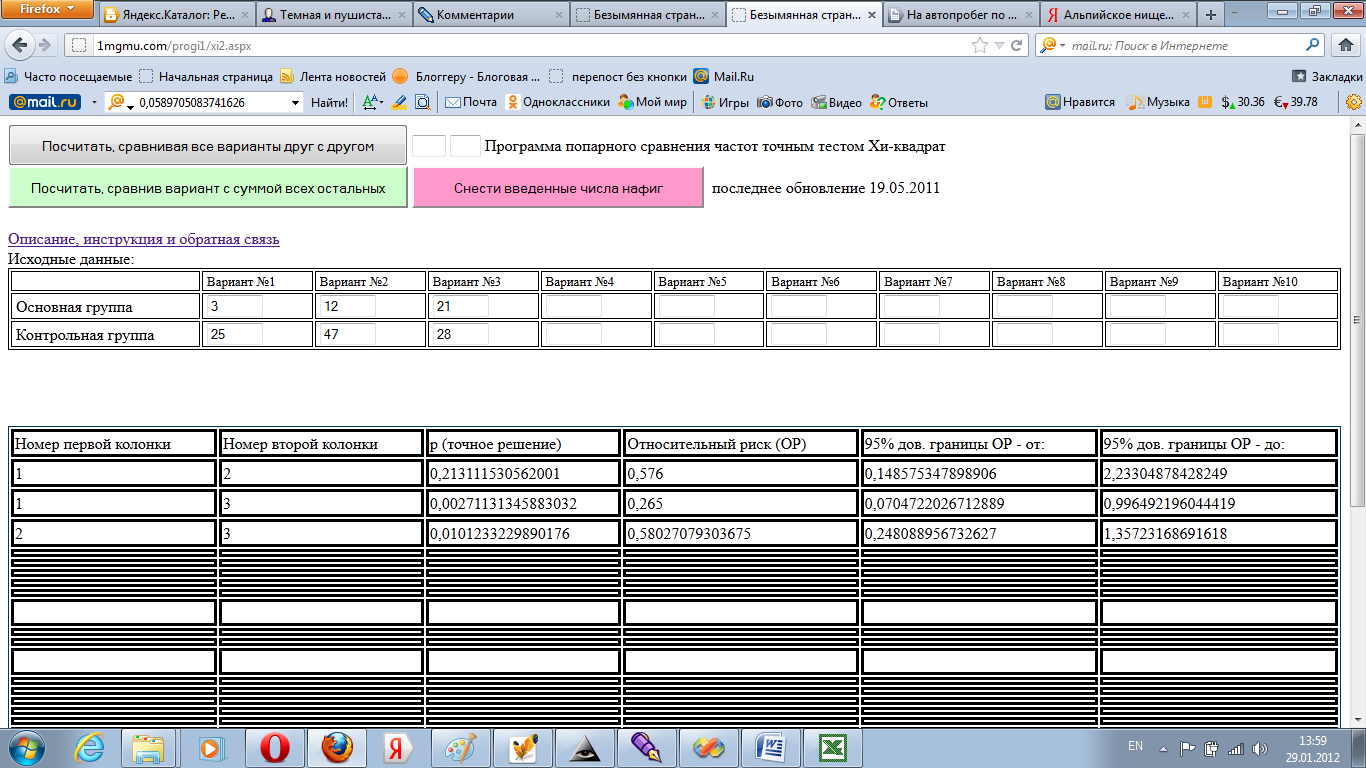
То есть первая строка – количества выживших, вторая – умерших. Для нужного варианта расчета нажать кнопку «Посчитать, сравнивая все варианты друг с другом»: В результате получаем:
Поиск по сайту: |
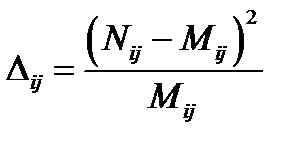 , суммируя их все, получаем общее различие
, суммируя их все, получаем общее различие 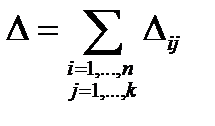 . В том случае, если выполняется нулевая гипотеза об одинаковости распределения исследуемых случайных величин, при числе наблюдений N®¥ распределение величины
. В том случае, если выполняется нулевая гипотеза об одинаковости распределения исследуемых случайных величин, при числе наблюдений N®¥ распределение величины  стремится к распределению
стремится к распределению 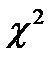 с числом степеней свободы (n-1)´(m-1). Практически пользоваться этим критерием можно, как и первоначальным вариантов, если общее число наблюдений не менее 50, а каждое из ожидаемых количеств M1,…, Mk не менее 5-7.
с числом степеней свободы (n-1)´(m-1). Практически пользоваться этим критерием можно, как и первоначальным вариантов, если общее число наблюдений не менее 50, а каждое из ожидаемых количеств M1,…, Mk не менее 5-7.