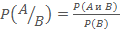I. Условные вероятности. Априорная и апостериорная вероятность

ЗАНЯТИЕ №2

Случайная величина задается тремя объектами: множеством элементарных событий, множеством событий и вероятностью событий.Те значения ,которые может принимать случайная величина, называются элементарными событиями.Наборы элементарных событий называются событиями. Для числовых и других не очень сложных случайных величин любой конкретно заданный набор элементарных событий есть событие.

Приведем пример: бросание игральной кости.

Всего имеется 6 элементарных событий: «очко», «2 очка», «3 очка»… «6 очков». Событие – любой набор элементарных событий, например «чет» -сумма элементарных событий «2 очка», «4 очка» и «6 очков».

Вероятность любого элементарного события P(A) равна 1/6:

вероятность события – количеству входящих в него элементарных событий, деленному на 6.

Достаточно часто в добавление к известной вероятности события имеется некоторая дополнительная информация, которая меняет эту вероятность. Например, летальность больных. поступивших в больницу с острой кровоточащей язвой желудка, составляет около 10%. Однако, если больному больше 80 лет, эта летальность составляет 30%.

Для описания таких ситуаций были введены так называемые условные вероятности. Они обозначаются, как P(A/B) и читаются «вероятность события А при условии события В». Для вычисления условной вероятности используется формула:

Вернемся к предыдущему примеру:

Пусть среди больных, поступивших в больницу с острой кровоточащей язвой желудка 20% - больные старше 80 лет. Причем, среди всех больных доля умерших больных старше 80 лет – 6%(напомним, что доля всех умерших составляет 10%). В этом случае

При определении условных вероятностей часто пользуются терминами априорной(буквально – до опыта) и апостериорной (буквально – после опыта) вероятности.

Пользуясь условными вероятностями, можно по одним вероятностям вычислить другие, например, менять местами событие и условие.

Рассмотрим эту технику на примере анализа связи риска заболевания ревматизма (ревматической лихорадкой) и одного из антигенов, являющихся для него фактором риска.

Частота заболевания ревматизмом – около 1%. Обозначим наличие ревматизма как R⁺ , тогда как P(R⁺)=0,01.

Наличие антигена будем обозначать, как А⁺. Его находят у 95% больных ревматизмом и у 6% лиц, ревматизмом не болеющих. В наших обозначениях это: условные вероятности Р(А⁺/R⁺)=0,95 и Р(А⁺/R^-)=0,06.

На основании этих трех вероятностей будем последовательно определять другие вероятности.

Прежде всего, если заболеваемость ревматизмом P(R⁺)=0,01, то вероятность не заболеть P(R^-)=1- P(R⁺)=0,99.

Из формулы для условной вероятности находим, что

Р(А⁺ и R⁺)= Р(А⁺/R⁺) * Р(R⁺) = 0,95*0,01 = 0,0095, или 0,95% популяции одновременно и болеют ревматизмом и имеют антиген.

Аналогично

Р(А⁺ и R^-)= Р(А⁺/R^-) * Р(R^-) = 0,06*0,99 = 0,0594, или 5,94% популяции носят антиген, но ревматизмом не болеют.

Так как все имеющие антиген или болеют ревматизмом или и не болеют (но не одновременно и то и другое), то сумма двух последних вероятностей дает частоту носительства антигена в популяции в целом:

Р(А⁺)= Р(А⁺ и R⁺) + Р(А⁺ и R^-) = 0,0095 + 0,0594 = 0,0689

Соответственно, доля людей, не имеющих антиген равна

Р(А^-)=1- Р(А⁺) = 0,9311

Так как заболеваемость ревматизмом равна 1%, а доля лиц, имеющих антиген и болеющих ревматизмом, равна 0,95%, то доля лиц, болеющих ревматизмом и не имеющих антигена равна:

Р(А^- и R⁺) = Р(R⁺) - Р(А⁺ и R⁺) = 0,01 – 0,0095 = 0,0005

Теперь будем двигаться в обратную сторону, переходя от вероятностей событий и их комбинаций к условным вероятностям. По исходной формуле условной вероятности Р(А⁺/R⁺)= Р(R⁺ и A⁺)/ Р(А⁺ ) = 0,0095/0,0689 » 0,1379 , или примерно 13,8% лиц, носящих антиген, заболеют ревматизмом. Так как заболеваемость популяции в целом лишь 1%, то факт выявления антигена повышает вероятность заболевания ревматизмом в 14 раз.

Аналогичным образом Р(R⁺ /А^-)=Р(R⁺ и A^-)/ Р(А^-) = 0,0005/0,9311 » 0,000054, то есть тот факт, что при проверке антигена не обнаружено, снижает вероятность заболевания ревматизмом в 19 раз.

Оформим эту задачу в электронной таблице Excel:

Можно посмотреть процесс построения таблицы картинки2\p2-1.gif

Поиск по сайту: