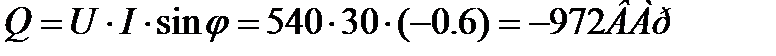|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Цепь с параллельным соединением электроприемников, содержащих активные, индуктивные и емкостные сопротивления
Комбинации сопротивлений электроприемников достаточно разнообразны, поэтому рассмотрим общие принципы расчета на примере параллельного соединения реальной индуктивной катушки и реального конденсатора (рис. 19)
Рисунок 19 - Параллельное соединение реальной индуктивной катушки и реального конденсатора Для такой цепи характерно то, что электроприемники, соединенные параллельно, находятся под общим напряжением. Ток каждой ветви определяется по закону где Z- полное сопротивление ветви Углы сдвига фаз φ1 и φ2 между током каждой ветви и напряжением определяются с помощью тригонометрических функций
Угол сдвига фаз обязательно следует проверять по синусу во избежание потери знака угла (косинус является четной функцией, но находить его тоже нужно. Он требуется в дальнейшем расчете цепи). Общий ток цепи, как следует из первого закона Кирхгофа, равен геометрической сумме токов ветвей На рис. 20 представлена векторная диаграмма этих токов.
Рисунок 20 – Векторная диаграмма токов
Общий суммарный или результирующий ток можно найти не только графически (в этом случае диаграмма должна быть построена в масштабе), но и математически, на основании теоремы Пифагора: где: Ia - проекция вектора общего тока на вектор напряжений он называется активной составляющей общего тока. IР - проекция вектора общего тока на линию, перпендикулярную линии напряжения, она называется реактивной составляющей общего тока Из диаграммы видно, что Iа = Ia1 + Iа2, Ip = - IC1 + IL2 В этих формулах: Ia1 и Iа2 - активные составляющие токов первой и второй ветви. IС1 - реактивная составляющая тока первой ветви. Она носит емкостный характер и поэтому взята со знаком «минус» IL2 - реактивная составляющая тока второй ветви. Она носит индуктивный характер и поэтому взята со знаком «плюс» Введем в формулу общего тока его составляющие, тогда:
Значение составляющих токов ветвей определить по формулам:
Активная мощность цепи равна арифметической сумме активных мощностей ветвей: Р = Р1+Р2,
Реактивная мощность цепи равна алгебраической сумме реактивных мощностей ветвей: Q =QL2 – QC1,
Активную и реактивную мощности цепи можно найти так:
где
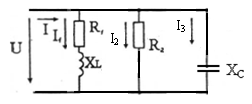
cos φ и sin φ используют также для определения угла сдвига фаз между общим током и напряжением Полная мощность цепи: Угол сдвига фаз φ между общим током и напряжением можно определить из выражения cos φ и sin φ используется также для определения угла сдвига фаз между общим током и напряжением. Пример 3 В электрической цепи (рис. 21) к источнику однофазного переменного синусоидального тока напряжением U=540В подключена катушка, обладающая активным R1=28,8 Ом и индуктивным сопротивлениями ХL = 21,6 Ом. Параллельно ей включены в одной ветви резистор с сопротивлением R2=45 Ом, в другой- конденсатор сопротивлением XC =20 Ом. Определить: токи в ветвях I1, I2 и I3; ток I, потребляемый цепью; угол сдвига фаз φ (по величине и знаку) между напряжением U и током I; активную Р, реактивную Q и полную S мощности цепи. Построить в масштабе векторную диаграмму токов.
Рисунок 21 – Электрическая схема
Решение 1 Полное сопротивление первой ветви Косинус и синус угла сдвига фаз φ2 между напряжением и током второй ветви
Ток второй ветви Активная и реактивная составляющие тока второй ветви
2 Во второй ветви дано только активное сопротивление, поэтому ее ток
Он совпадает по фазе с напряжением и носит активный характер. Угол сдвига фаз между этим током и напряжением φ1= 0. Реактивная составляющая тока в этой ветви отсутствует 3 В третьей ветви дано только ёмкостное сопротивление, поэтому её ток
Этот ток опережает напряжение на угол φ = - 90°. Активная составляющая тока этой ветви равна нулю 3 Определяем ток в неразветвленной части цепи
4 Определяем коэффициент мощности всей цепи Угол сдвига фаз находим по синусу во избежание потери знака угла (косинус является четной функцией):
5 Активные и реактивные мощности элементов:
6 Полная мощность цепи. Проверка 7 Для построения векторной диаграммы напряжений зададимся масштабами mU=100В/см, mI=3А/см. Векторная диаграмма представлена на рис.22. 8 Измеряем вектор суммарного тока lI=6см,тогда I=lI..mI=7,1.0,28=2А и убеждаемся в том, что с учетом масштаба его величина равна току, определенному математическим путём.
Рисунок 22 – Векторная диаграмма токов
Поиск по сайту: |



 и
и 
 ;
; 
 ;
; 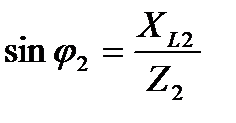








 или
или 
 или
или 
 или
или 
 или
или 
 или
или 
 или
или 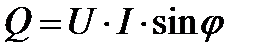 ,
,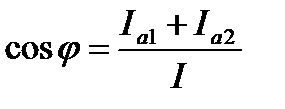 и
и 
 или
или 
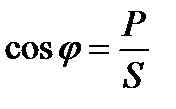 и
и  , а также
, а также  и
и 

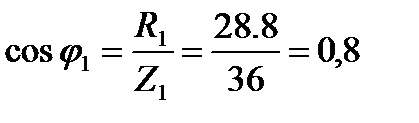 .
. 





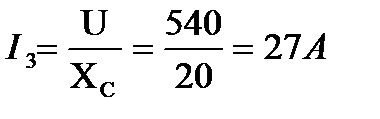
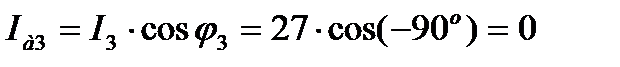


 тогда: φ= 37°
тогда: φ= 37°