 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сформулируйте теорему о достаточном условии оптимальности опорного решения.
Теорема (достаточное условие оптимальности опорного решения) Если для опорного решения α0 канонической задачи линейного программирования на минимум (1) – (3) найдется базис, для которого все оценки неположительные, то есть δj≤0 для всех j = 1, 2, …, n, то вектор α0 является оптимальным решением данной задачи. Доказательство Пусть δ1, δ2, …, δn – оценки системы векторов условий, приведенных к некоторому базису опорного решения α0. Если вектор β=( Так как, для любых j=1, 2, …, n по условию δj≤0 , а вектор β=( Сформулируйте теорему о неограниченности целевой функции КЗЛП. Теорема ( о неограниченности целевой функции). Пусть симплекс таблица приведена к некоторому базису опорного решения α канонической задачи линейного программирования (1) – (3) на минимум. Если при этом существует столбец Аs с положительной оценкой, т.е. δs > 0, где s=1, 2, …, n , а все остальные элементы этого столбца неположительные, т.е, αis ≤ 0, i=1, 2, …, r , то целевая функция данной задачи неограниченна на множестве допустимых решений, и, следовательно, задача не имеет оптимального решения. Доказательство Пусть симплекс таблица приведена к базису А1, А2, …, Аr опорного решения α=(α1, α2, …, αr, 0, 0, …, 0) и имеет вид:
Следовательно, вектор ограничений В’, а также вектор условий А’s можно представить в виде линейной комбинации базисных векторов, а именно, (12)А’1 α1+ А’2 α2 + …+ А’r αr = В’ и А’1 a’1s + А’2 a’2s + … + А’r a’rs = A’s
(13)А’1 a’1s + А’2 a’2s + … + А’r a’rs – A’s =Ө . Помножив соотношение (13) на переменную t > 0 и вычтя его из соотношения (12), получим: А’1 ( α1 – t a’1s ) + А’2 ( α2 – t a’2s ) + … + А’r (αr – t a’rs) + A’s t = B’. Из последнего соотношения и с учетом того, что a’is ≤ 0, следует, что вектор Αt = (α1 – t a’1s , α2 – t a’2s , …, αr – t a’rs , 0, …, 0, t, 0, …, 0 ) является допустимым решением задачи (1) – (3). По лемме о целевой функции для допустимого решения αе имеем f(αt) = f(α) – δ1 ( α1 – t a’1s ) – δ2 ( α2 – t a’2s ) – …– δr ( αr – t a’rs ) – δs t . С учетом того, что оценки базисных векторов равны нулю, т.е., δ1= δ2= …= δr=0, значение целевой функции можно записать в виде: f(αt) = f(α) – δs t. Так, как δs > 0 , то при t→ +
Поиск по сайту: |
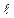 1, …,
1, …, 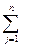 δj
δj 
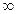 целевая функция неограниченно уменьшается, т.е., f(αt) → –
целевая функция неограниченно уменьшается, т.е., f(αt) → –