 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сформулируйте теорему о существовании опорного решения.
Теорема(о существовании опорного решения). Если каноническая задача линейного программирования имеет хотя бы одно допустимое решение, то эта задача имеет и опорное решение. Доказательство Рассмотрим КЗЛП (1)f(X) = (2) (3)xj ≥ 0, j = 1,2,…,n, которая имеет хотя бы одно допустимое решение. Из всех допустимых решений данной задачи выберем допустимое решение с наименьшим числом ненулевых координат. Пусть таким решением будет вектор α = ( α1, …, α Предположим противное, а именно, что вектор α не является опорным решением. Тогда по определению опорного решения, векторы A1, A2, … A (1)A1 k1 + A2 k2 + … + A Так как вектор α является допустимым решением рассматриваемой задачи, то по определению, этот вектор является решением системы линейных уравнений (2). Тогда по определению решения системы уравнений должно выполняться соотношение (2)A1 α 1 + A2 α 2 + … + A Прибавив к соотношению (5) соотношение (4), умноженное на А1( α1 Из последнего соотношения по определению решения системы уравнений следует, что векторы α’ = ( α1 + δ k1, α2 + δ k2, … α
Сколько базисов системы векторов условий КЗЛП может соответствовать одному опорному решению? Любому опорному решению канонической задачи линейного программирования соответствует, по крайне мере, один базис системы векторов условий этой задачи. Доказательство Пусть вектор α = ( 0, …,0, α i1 , 0,…, 0, αi2 , 0, …, 0, αil, 0, …, 0 ) является опорным решением канонической задачи линейного программирования (1)f(X) = (2) (3) xj ≥ 0, j = 1, 2, …, n. где α i1>0 , αi2>0, …, αi
Поиск по сайту: |
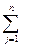 γj xj + γ0,
γj xj + γ0,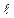 , 0, …, 0), где координаты α1> 0, …, α
, 0, …, 0), где координаты α1> 0, …, α  δ, получим
δ, получим