 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сколько ненулевых координат может иметь опорное решение?
Число ненулевых координат у любого опорного решения α канонической задачи линейного программирования не превышает r = rang{ A1, …, An } – ранга системы векторов условий этой задачи. Доказательство Пусть вектор α = ( 0, …,0, α i1 , 0,…, 0, αi2 , 0, …, 0, αil, 0, …, 0 ) является опорным решением канонической задачи линейного программирования (1)f(X) = (2) (3) xj ≥ 0, j = 1, 2, …, n. где α i1>0 , αi2>0, …, αi Выше было доказано, что любому опорному решению КЗЛП соответствует хотя бы один базис системы векторов условий КЗЛП. Число векторов в любом базисе системы векторов условий КЗЛП совпадает с рангом этой системы. По определению базиса опорного решения, все координаты опорного решения α, соответствующие не базисным векторам системы векторов условий КЗЛП , равны нулю. Следовательно, ненулевых координат у опорного решения α не более, чем r.
Чему соответствуют элементы столбца ограничений В симплекс-таблицы, приведенной к базису опорного решения? Если симплекс таблица приведенна к базису Аi1. Аi2, … , Аir опорного решения α, то в столбце В’ находятся координаты опорного решения α, соответствующие векторам базиса Аi1. Аi2, … , Аir , то есть α1’ = αi1, α2’ = αi2, …, αr’ = αir, Доказательство Так как вектор α = ( 0, 0, …, 0, αi1, 0, 0, …, 0, αi2, 0, 0, …, 0, αir, 0, 0, .., 0) является опорным решением задачи (1) – (3), то он является и допустимым решением этой задачи, а следовательно, является решением системы линейных уравнений (2), то есть выполняется соотношение: (6) Аi1 αi1+ Ai2 αi2+…+ Air αir = B. Решением системы (5) является вектор α’ = ( 0, 0, …, 0, α1’, 0, 0, …, 0, α2’, 0, 0, … , 0, αr’, 0, 0, .., 0). Системы (5) и (4) равносильны, так как получены одна из другой методом Гаусса. Поэтому вектор α’ является решением системы (4), и, следовательно, выполняться соотношение: (7) Аi1 α1’+ Ai2 α2’+…+ Air αr’ = B. Вычитая из соотношения (6) соотношение (7), получаем соотношение: (8)Аi1 (αi1 – α1’ )+ Ai2 (αi2 – α2’ )+…+ Air (αir – αr’ ) = Ө. Так как векторы Аi1. Аi2, … , Аir являются базисом системы векторов условий задачи (1) – (3), то они линейно независимы. Следовательно, соотношение (8) возможно, при αi1 – α1’ = 0, αi2 – α2’ = 0, …, αir – α1’ = 0. Откуда αi1 =α1’, αi2 = α2’, …, αir = α1’
Поиск по сайту: |
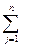 γj xj + γ0,
γj xj + γ0,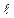 > 0. Тогда по определению в системе векторов условий задачи (1) – (3) векторы Ai1, Ai2, …, Ai
> 0. Тогда по определению в системе векторов условий задачи (1) – (3) векторы Ai1, Ai2, …, Ai