ТЕСТЫ САМОКОНТРОЛЯ ЗНАНИЙ. (ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ)

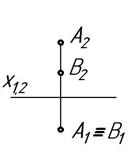
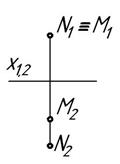
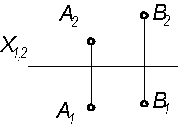
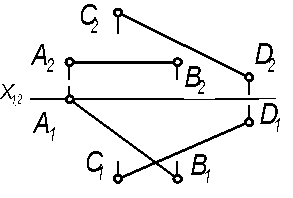
(ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ)

1 Заданные точки, являющиеся конкурирующими относительно плоскости П₂, изображены на рисунке:

1) 2) 3) 4) Ответ:

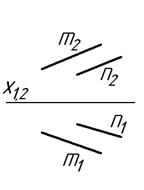
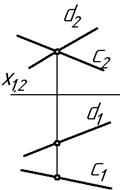
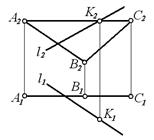
2 Параллельные прямые изображены на рисунке:

1) 2) 3) 4) Ответ:

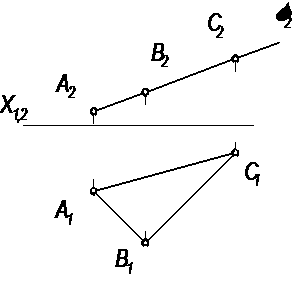
3 На каком чертеже правильно построена точка К пересечения прямой ℓ с плоскостью АВС и показана видимость прямой?

Ответ:

4 Прямая l, принадлежащая плоскости треугольника АВС, изображена на рисунке:

1) 2) 3) Ответ:

5 Взаимно параллельные плоскости изображены на рисунке:

1) 2) 3) Ответ:

ТЕМА 4 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА

Вопросы самоконтроля:

1. Как выбирают новую плоскость проекций относительно оставшейся плоскости и по отношению к геометрической фигуре?

2. Сколько плоскостей проекций можно заменить одновременно?

3. Какие задачи решаются заменой одной плоскости проекций?

4. Как прямую общего положения преобразовать в прямую уровня?

5. Как плоскость общего положения преобразовать в проецирующую?

6. Как плоскость общего положения преобразовать в плоскость уровня?

7. Какие задачи решаются двумя заменами плоскостей проекций?

УПРАЖНЕНИЯ

6.1 Построить проекции точек А и В в новой системе П₁/П₄.

6.2 Прямую общего положения преобразовать в положение горизонтали. Определить натуральную величину отрезка.

6.3 Отрезок АВ преобразовать в положение проецирующего.

ЗАДАЧИ

6.4 Определить натуральную величину треугольника АВС, лежащего в плоскости S(S₂).

6.5 Дана фронтальная проекция точки А, удаленной от плоскости S (f ∩ h) на

20мм. Построить горизонтальную проекцию точки А.

6.6 Построить проекции (К₁,К₂) точки К пересечения прямой l с плоскостью S(ABC). Определить видимость прямой l на плоскостях П₁ и П₂.

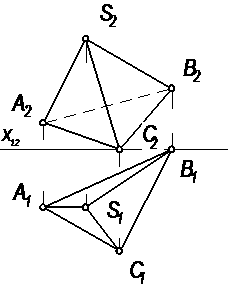
6.7 Определить расстояние от вершины S пирамиды SABC до ее основания ABC. Построить проекции высоты пирамиды на плоскостях П₁ и П₂.

6.8 Построить проекции (М₁N₁, М₂,N₂) отрезка МN, определяющего расстояние между прямыми АВ и СD.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1Преобразовать прямую общего положения в прямую уровня

Решение:

Алгоритм графических построений:

1. Проводим ось проекций П1П4 параллельно А1В1 и на произвольном расстоянии от А1В1;

2. проводим линии проекционной связи в системе плоскостей проекций П1П4 перпендикулярно оси П1П4;

3. откладываем на них от оси П1П4 расстояния равные расстояниям от А2 и В2 до оси П1П2;

4. соединяем А4 и В4.

Длина проекции А4В4 равна длине отрезка АВ. Угол α - угол наклона АВ к оси П1П4 равен углу наклона АВ к плоскости проекций П1.

Задача 2Преобразовать плоскость общего положения в плоскость уровня.

Решение:

Преобразуем плоскость общего положения в проецирующую введением дополнительной плоскости проекций П4. На П4 плоскость АВС проецируется линией. Теперь нам следует ввести еще одну дополнительную плоскость проекций П5 параллельно плоскости АВС. В системе плоскостей П4П5 плоскость АВС является плоскостью уровня, так как параллельна П5. Обратите внимание, что треугольник АВС проецируется на плоскость П5 в натуральную величину.

Алгоритм графических построений:

1.Проводим проекцию М2N2 некоторой прямой, принадлежащей плоскости АВС:M2N2 ║П1П2;

2. проводим линии проекционной связи и находим проекциюM1N1 этой прямой на П1;

3. проводим ось проекций П1П4 на произвольном расстоянии и перпендикулярно M1N1;

4. проводим линии проекционной связи в системе плоскостей проекций П1П4 перпендикулярно оси П1П4;

5. откладываем на них от оси П1П4 расстояния равные расстояниям от А2, В2, С2 и M2N2 до оси П1П2;

6. соединяем точки и получаем проекцию плоскости АВС на П4;

7. проводим ось проекций П1П4 на произвольном расстоянии и параллельно С4В4;

8. проводим линии проекционной связи в системе плоскостей проекций П4П5 перпендикулярно оси П4П5;

9. откладываем на них от оси П4П5 расстояния равные расстояниям от А1, В1, С1 и M1N1 до оси П1П4;

10. соединяем точки и получаем проекцию плоскости АВС на П5.

Поиск по сайту: