ТЕСТЫ САМОКОНТРОЛЯ ЗНАНИЙ (ТОЧКА)

1В каком случае точка принадлежит прямой?

1) одноименные проекции точки принадлежат одноименным проекциям прямой

2) одна из одноименных проекций точки принадлежит одноименной проекции прямой, а другая нет

3) разноименные проекции точек принадлежат разноименным проекциям прямой. Ответ:

2Точка А находиться в квадранте:

1) в I

2) во II

3) в III

4) в IV Ответ:

3Точка А, принадлежащая плоскости П₂ , изображена на рисунке:

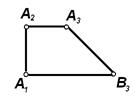
1) 2) 3) 4) Ответ:

4 Заданные точки, являющиеся конкурирующими относительно плоскости П₂, изображены на рисунке:

.. ..... .....

1) 2) 3) 4) Ответ:

5 Какие из точек: A, B, C, D принадлежат одной плоскости?

1) А и В

2) В и С

3) В и D

4) А и D Ответ:

6 У какой из точек равны все три координаты?

1. В

2. С

3. D

4. Е

Ответ:

Комплексный чертеж прямой

УПРАЖНЕНИЯ

3.2.1 При каком условии точка В (осевая проекция В_х которой задана) принадлежит линии 1?

3.2.2 Построить проекции отрезка АВ по заданным проекциям точек А и В. Известны разности координат этих точек: YА – YВ = 10; ZВ – ZА = 5.

3.2.3 Построить проекции отрезка АВ, который является фронталью, и отрезка АС, который является горизонталью.

3.2.4 На прямой m построить точку, одинаково удаленную от плоскостей П₁ и П₂.

ЗАДАЧИ

3.2.5 Найти натуральную величину отрезка АВ и углы его наклона к плоскостям П₁, П₂. Координаты точек отрезка А (60, 5, 10), В (10, 20,40).

3.2.6 На отрезке АВ определить точку С, которая делит отрезок внутренним образом в заданном отношении: СА:СВ= 2 : 5.

3.2.7 Постройте на комплексном чертеже два отрезка соответственно пересекающихся, параллельных, скрещивающихся и конкурирующих прямых.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ:

Задача 1Построить прямую параллельную:

а) горизонтальной плоскости проекций

Решение:

Прямая параллельная горизонтальной плоскости проекций, называется горизонталью - h.На горизонтальную плоскость проекций горизонталь проецируется в натуральную величину.

б) фронтальной плоскости проекций

Решение:

Прямая параллельная фронтальной плоскости проекций, называется фронталью - f.На фронтальную плоскость проекций фронталь проецируется в натуральную величину.

Задача 2 Построить комплексный чертеж двух прямых:

а) пересекающихся:

Решение:

Нам даны пересекающиеся прямые a и b. K - точка пересечения прямых a и b. Построим чертеж. Отметим точку К. Раз точка К принадлежит обеим пря мым, то проводим проекции прямых a и b через одноименные проекции точки их пересечения. Свойство: если прямые пересекаются, то точки пересечения их одноименных проекций находятся на одной линии связи.

б) параллельных:

Решение:

Нам даны параллельные прямые АВ // СD их проекции также параллельны. Свойство:параллельность отрезков прямых сохраняется в проекциях.

в) скрещивающихся:

Решение:

Скрещивающиеся прямые не принадлежат одной плоскости, т.е. не пересекаются и не параллельны. Свойство:точки пересечения проекций прямых не лежат на одной линии связи.

ТЕСТЫ САМОКОНТРОЛЯ ЗНАНИЙ (ПРЯМАЯ)

1 Как называется прямая параллельная горизонтальной плоскости проекций?

1) фронтальная прямая

2) горизонтальная прямая

3) профильная прямая Ответ:

2 Как называется прямая параллельная фронтальной плоскости проекций?

1) горизонтальная прямая

2) профильная прямая

3) фронтальная прямая Ответ:

3 Как расположена горизонтально – проецирующая прямая относительно плоскостей проекций?

1)║ П₁ 2) ┴ П₂ 3) ┴ П₁ 4)║ П₃ Ответ:

4Если две прямые в пространстве параллельны, то их одноименные проекции:

1) параллельны 2) пересекаются 3) скрещиваются Ответ:

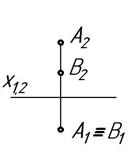
5 Прямой l принадлежит точка:

1) А

2) В

3) С

4) D Ответ:

6 Отрезками частного положения являются:

1) АВ и EF

2) CD и DE

3) AB, ВС и DE

4) BC, EF и AB

Ответ:

7 Горизонтальная прямая изображена на рисунке:

1) 2) 3) 4) Ответ:

8 Укажите комплексный чертеж отрезка прямой общего положения?

Ответ:

9 На каком чертеже ни одна из проекций не дает истинной длины отрезка АВ?

Ответ:

Поиск по сайту: