 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Необходимость случайного изменения стратегии в игре без седловой точки
Смешанной стратегией SA игрока А называется применение чистых стратегий A1, A2, ..., An с вероятностями p1, p2, ..., pi, ..., pn причем сумма вероятностей равна 1:
или в виде строки SA=(p1, p2, …, pn). В отличие от смешанных стратегий SA стратегии Aj называют чистыми. При надлежащем подборе вероятностей pj смешанная стратегия может оказаться оптимальной. При этом выигрыш игрока A будет не меньше некоторого значения v, называемого ценой игры. Это значение больше нижней цены игры, но меньше верхней. Аналогичны образом должен вести себя игрок B. Его оптимальная стратегия также есть некоторая смешанная стратегия
или в виде строки SB=(q1, q2, …,qm), где qj — специально подобранные вероятности, с которыми игрок B использует стратегии Bj. Сумма вероятностей равна 1: Чистые стратегии можно считать частным случаем смешанных. На основании принципа минимакса определяется оптимальное решение (или решение) игры: это пара оптимальных стратегий S*A, S*B в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству α≤v≤β, где α и β — нижняя и верхняя цены игры. Справедлива следующая основная теорема теории игр — теорема Неймана. Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий. Пусть S*A = (p*1, p*2, ..., p*i, ..., p*m) и S*B = (q*1, q*2, ..., q*i, ..., q*n) — пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной. Справедлива теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий. Решением игры называется такая пара стратегий — в общем случае смешанных, систематическое применение которых обеспечивает каждой стороне максимально возможный для нее по условиям игры выигрыш, определяемый ценой игры. Если же одна из сторон отступает от своей оптимальной стратегии (в то время как другая продолжает придерживаться своей), то это ни в коем случае не может быть выгодно для отступающего; это либо оставит его выигрыш неизменным, либо уменьшит. Таким образом, каждая конечная игра имеет решение (возможно, в области смешанных стратегий). Это положение называется основной теоремой теории игр. Эта теорема имеет большое практическое значение — она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки. Графические приемы выбора оптимальной смешанной стратегии. Отличие выбора смешанной стратегии при конфликте от выбора смешанной стратегии в ситуации неопределенности. Байесовский анализ намерений противника. Графические методы решения игр. Для определенности положим, что игрок I имеет возможность выбирать между двумя стратегиями с вероятностями x1 и x2 = 1-x1, тогда его ожидаемые выигрыши, соответствующие чистым стратегиям игрока II, примут вид
Или
Линии, изображенные на рис. 6.1, задают зависимости среднего выигрыша игрока I от значения вероятности x1 , с которой он выбирает свою первую стратегию, для случаев, когда его противник выбирает первую, вторую или третью чистую стратегию. Тогда значениям минимального гарантированного дохода первого игрока соответствует нижняя огибающая всех трех прямых. Согласно принципу максимина, оптимальному выбору игрока I будет соответствовать наивысшая точка, лежащая на данной огибающей, отмеченная на рисунке как (x1*, z*). Зная ее, можно определить оптимальную смешанную стратегию первого игрока х* = (x1*, 1-x2*) и цену игры, равную z*. Исходя из отношения двойственности, которым, как было установлено в п. 6.1.5, связаны задачи обоих игроков, по оптимальной стратегии первого участника х* однозначно определяется оптимальная стратегия его противника у*. Поскольку у* является результатом решения задачи линейного программирования, то он обладает всеми свойствами допустимого базисного плана, т. е. в случае 2 х п игры имеет не более чем две ненулевых компоненты и не менее чем (п-2) нулевых. Номера ненулевых элементов у* определяются номерами линий, пересечение которых определило оптимальную стратегию первого игрока. Действительно, игрок II знает оптимальную стратегию соперника, и применение им стратегий, соответствующих прямым, проходящим выше точки (х1*, z*), только увеличило бы его проигрыш. В рассматриваемом примере это линии z2 и z3, и, следовательно, в своей оптимальной стратегии второй игрок должен с ненулевыми вероятностями применять вторую и третью чистые стратегии (у2>0, у3 >0). На основе этого, а также учитывая условие нормировки
можем выразить: y3 = l – y2 тогда оптимальное значение y2* может быть найдено из условия
В результате получаем оптимальную стратегию игрока II у*= (0, у2*, у3*). Очевидно, что поиск решения в игре т х 2 осуществляется аналогичным образом с точностью до наоборот: строятся графики ожидаемого проигрыша игрока II, находится их верхняя огибающая и т. д. Безусловно, графический способ в силу ограниченности круга задач, к которым он может быть применен, имеет скорее теоретическое, чем практическое значение. Однако он хорошо иллюстрирует содержательную сторону процесса поиска решения в игре. Критерий ожидаемого значения(критерий Байеса-Лапласа) Использование данного критерия обусловлено стремлением максимизировать ожидаемую прибыль (или минимизировать ожидаемые затраты). Математически это выглядит так: пусть ξ – случайная величина с математическим ожиданием Mξ и дисперсией Dξ. Если x1, x2,..., xn – значения случайной величины (с.в.) ξ, то среднее арифметическое их (выборочное среднее) значений
имеет дисперсию
Другими словами при достаточно большом объёме выборки разница между средним арифметическим и математическим ожиданием стремится к нулю (так называемая предельная теорема теории вероятности). Следовательно, использование критерия "ожидаемое значение" справедливо только в случае, когда одно и то же решение приходится применять достаточно большое число раз. Верно и обратное: ориентация на ожидания будет приводить к неверным результатам, для решений, которые приходится принимать небольшое число раз. Таким образом, если вероятности состояний природы известны и не изменяются со временем (стационарны), то оптимальным следует считать решение, максимизирующее ожидаемый выигрыш (которое дает наибольшее математическое ожидание выигрыша против известной стратегии природы – состояния или условия).
Поиск по сайту: |
 Смешанные стратегии игрока А записываются в виде матрицы
Смешанные стратегии игрока А записываются в виде матрицы ,
,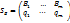
 При выборе игроком B оптимальной смешанной стратегии выигрыш игрока A будет не больше цены игры v.
При выборе игроком B оптимальной смешанной стратегии выигрыш игрока A будет не больше цены игры v.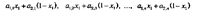

 т. е. ожидаемые выигрыши могут быть представлены в виде графиков линейных функций, зависящих от переменной x1 ∊ [0; 1] (рис. 6.1, где предполагается, что игрок II имеет три стратегии).
т. е. ожидаемые выигрыши могут быть представлены в виде графиков линейных функций, зависящих от переменной x1 ∊ [0; 1] (рис. 6.1, где предполагается, что игрок II имеет три стратегии).
 или
или

 . Таким образом, когда n→
. Таким образом, когда n→ 
 →Mξ.
→Mξ.