|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОБЩЕТЕОРЕТИЧЕСКИЕ ОСНОВЫ КУРСАСтр 1 из 26Следующая ⇒
Г.А. Тихановская, Е.А. Фокичева
ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ РАЗВИТИЯ И ТУШЕНИЯ ПОЖАРОВ Часть1 Утверждено редакционно - издательским советом ВоГТУ в качестве учебного пособия
Вологда УДК ББК Т
Рецензенты: Т.Л. Бланк, канд. хим. наук, доцент Вологодской молочнохозяйственной академии им. Н.В. Верещагина; М.Б. Гусев, ст. преп. Вологодского государственного педагогического университета. Тихановская, Г.А. Физико-химические основы развития и тушения пожаров:учеб. пособие / Г.А. Тихановская, Е.А. Фокичева. – Вологда: ВоГТУ, 2012. - 118 с.
Учебное пособие по курсу «Физико-химические основы развития и тушения пожаров» часть I предназначено для студентов направления бакалавриата 280700 «Техносферная безопасность», профиль «Защита в чрезвычайных ситуациях». Пособие составлено в соответствии с программой курса и может быть использовано как руководство для самостоятельной работы студентов. В пособии включено краткое изложение курса по теме «Горение», руководство к лабораторным работам и тематические тесты для проверки знаний. Может быть использовано как при текущей проверке усвоения материала, так и при подготовке к экзаменам студентами направления «Техносферная безопасность».
УДК ББК
ВоГТУ, 2012 Тихановская Г.А., Фокичева Е.А. 2012 ПРЕДИСЛОВИЕ Учебное пособие «Физико-химические основы развития и тушения пожаров» составлено для студентов направления бакалавриата «Техносферная безопасность», профиль «Защита в чрезвычайных ситуациях». Пособие включает общетеоретические основы курса, теоретические вопросы и методологию изучения процессов горения и пожаротушения. Тематические тесты затрагивают все аспекты рассматриваемого курса и могут быть использованы для закрепления материала и при подготовке к экзаменам. ВВЕДЕНИЕ Горение используется человеком на протяжении более миллиона лет и является одной из древнейших технологий. В настоящее время около 90% всей энергии, потребляемой нашей цивилизацией (выработка электроэнергии, получение топлива, транспорт и т.д.), обеспечивается процессами горения. Но неконтролируемый процесс горения (пожар) обладает огромной разрушающей силой и приводит к катастрофическим последствиям. Пожары – самые распространенные чрезвычайные происшествия. Действие их многостороннее: взрывы, обрушения конструкций, радиационное и химическое загрязнение атмосферы, почвы, гибель флоры и фауны. Пожары сопровождаются потреблением кислорода из воздуха, образованием продуктов горения, в том числе и токсичных, и поступление их в атмосферу, использованием воды для целей пожаротушения, распространением водяных паров и отработанной воды с растворенными в них токсичными продуктами на обширную территорию. В основе большинства из указанных процессов лежат физико-химические закономерности, поэтому является необходимым рассмотрение фундаментальных концепций, связанных с вопросами химии горения, стехиометрическими расчетами, законами термодинамики, теории скоростей химических реакций и т.д. А также прикладное значение вышеуказанных закономерностей для классификации пожаров, определения средств пожаротушения и оптимизации действия пожаров и их последствия для людей и окружающей среды. В связи с этим в данном пособии рассматриваются общетеоретические основы курса, агрегатные состояния веществ, термодинамические законы, материальный и тепловой баланс процессов горения. А также явления, сопровождающие пожар, динамика развития пожара и опасные факторы пожара. ОБЩЕТЕОРЕТИЧЕСКИЕ ОСНОВЫ КУРСА Агрегатные состояния Состояние данной массы газа определяется тремя величинами (параметрами): давлением p, объемом V и температурой T. Эти величины связаны между собой функциональной зависимостью, которая может быть представлена соотношением f (p, V, T) = 0, называемым уравнением состояния. Уравнение состояния идеального газа выводится из трех законов – Бойля – Мариотта, Гей-Люссака и Авогадро. Реальные газы подчиняются этим законам тем точнее, чем меньше давление и выше температура. Закон Бойля – Мариотта. При постоянной температуре объем данной массы обратно пропорционален давлению. Если V1 и V2 – объемы газа при давлении p1 и p2 соответственно, то
Из закона Бойля – Мариотта вытекает следствие: при постоянной температуре плотность газа ρ пропорционально его давлению:
Законы Гей-Люссака и Шарля. При постоянном давлении с повышением температуры на 1°С объем данной массы газа увеличивается на 1/273,15 его объема при 0°С:
где V – объем газа при температуре t °С, а V0 – объем газа при 0°С. При замене шкалы Цельсия абсолютной температурной шкалой (шкалой Кельвина), для которой T=273,15+t, этот закон можно сформулировать следующим образом: при постоянном давлении объем данной массы газа пропорционален его абсолютной температуре:
где V1 и V2 – объемы газа при абсолютных температурах T1 и T2 При постоянном объеме зависимость давления данной массы газа от температуры записывается уравнениями, аналогичными (1.2) и (1.3):
Объединенный закон Бойля – Мариотта – Гей-Люссака выражается уравнением:
где p1 – давление и V1 – объем данной массы газа при абсолютной температуре T1, p2- давление и V2 – объем той же массы газа при абсолютной температуре T2. Закон Авогадро: в равных объемах различных газов при одинаковых условиях содержится равное число молекул. Число молекул (NA) в 1 моль вещества одинаково у всех веществ и равно 6,02·1023 (число Авогадро). Следовательно, количества веществ 1 моль, находящихся в газообразном состоянии при одинаковой температуре и одинаковом давлении, занимают равные объемы. При нормальных условиях (температура 0°С и давление = 1,01325·105 Па) объем 1 моль газа равен 22,414л. Уравнение состояния идеального газа – уравнение Менделеева – Клайперона для одного моля газа имеет вид:
а для любого количества газообразного вещества:
где R – универсальная газовая постоянная, числовое значение которой зависит от единиц измерения других величин. Величина ее выражается в единицах СИ Дж/(моль·К). Уравнение (1.8) может быть использовано для определения относительной молекулярной массы Мч. Заменяя в нем величину n отношением m/M, где m – масса газа, а M – молярная масса данного газа, и решая его относительно M, получим:
Закон Дальтона: общее давление смеси газов равно сумме парциальных давлений составных частей (компонентов):
где pоб – общее давление смеси газов, p1, p2, pk – парциальные давления компонентов смеси. Парциальным давлением называется давление каждого компонента, если бы он один занимал объем, равный объему смеси той же температуре. Уравнения (1.8) и (1.9) применимы к смесям газов, химически не взаимодействующих друг с другом, а также к каждому компоненту смеси. В первом случае n – общее количество вещества компонентов (n=n1+n2+…+nk=∑ni, где i=1, 2, …, k), M – средняя «смешанная» молярная масса, во втором случае n – количество вещества каждого компонента, т.е. n1, n2, …, nk, p – парциальное давление компонента, V – общий объем смеси. Зависимость между парциальными давлениями и общим выражается уравнениями:
Отношения n1/∑ni, n2/∑ni, …, nk/∑ni, называют молярными долями данного компонента. Если молярную долю обозначить через x, то парциальное давление любого i-го компонента смеси (где i = 1, 2, …, k) будет равно:
Таким образом, парциальное давление каждого компонента равно произведению его молярной доли на общее давление смеси. Для идеальных газов молярная доля x равна объемной доле φ (V1/∑υi, V2/∑υi, …, Vk/∑υi). Если состав смеси выражен в объемных долях (%), то φ' φ1'/100 = x1, φ2'/100 = x2, …, φk'/100 = xk, (1.12) Кинетическая теория газов. Основным уравнением кинетической теории газов для 1 моль является уравнение:
где ma – масса молекулы; ū – средняя квадратичная скорость молекул; NA – число молекул в 1 моль. Для любого количества вещества в уравнении вместо NA входит N. Из основного уравнения кинетической теории газов можно вывести изложенные выше газовые законы и некоторые новые положения. Сопоставляя уравнения (I, 7) и (I, 13) получим для 1 моль газа:
1. Отсюда находим среднюю квадратичную скорость молекул:
где M = NA·ma – молярная масса газа. Из этого уравнения следует, что для одного и того же газа средняя квадратичная скорость молекул прямо пропорциональна корню квадратному из абсолютной температуры:
где ū1 – средняя квадратичная скорость при температуре T1, а ū2 –то же самое при T2. Для различных газов при одинаковой температуре средняя квадратичная скорость молекул обратно пропорциональна корню квадратному из относительных молекулярных масс:
Здесь ū1 и 2. Из уравнения (1.14) находим:
Выражение, стоящее в левой части этого равенства, есть средняя кинетическая энергия поступательного движения молекул идеального газа в количестве вещества 1 моль. Обозначив ее через Е, получим:
Разделив обе части уравнения (1.18) на NA, найдем, что средняя кинетическая энергия поступательного движения одной молекулы газа равна:
где Следовательно, кинетическая энергия идеального газа пропорциональна абсолютной температуре. Примеры 1.В баллоне емкостью 20 л находится водород под давлением 162·105 Па. Сколько шаров-пилотов можно наполнить водородом, если объем шара равен 200 л и давление в нем должно быть равно 2·105 Па? Водород при этих условиях считать идеальным газом. Решение. Так как температура и масса газа остаются постоянными, то для решения задачи применим закон Бойля – Мариотта (1.1). После наполнения шаров-пилотов объем водорода (V2) буде равен:
где V3 – объем одного шара; n – число шаров; V1 – объем баллона, в котором водород после наполнения последнего шара находится под давлением 2·105 Па. Заменив в уравнении (1.1) V2 его значением, получим:
Отсюда
Находим, что водородом можно наполнить восемь шаров-пилотов. 2.При нормальных условиях плотность азота равна 1,25 г/л. Определить плотность газа при 0°С и давлении 5,065·105 Па. Решение. Требуется определить плотность азота при 0°С и давлении 5,065·105 Па. Из уравнения (I, 1а) находим ρ2 – плотность при давлении p2:
3. При постоянном давлении открытая двухлитровая колба охлаждается от 200 до 0°С. Насколько увеличится масса воздуха в колбе, если плотность воздуха при нормальных условиях равна 1,293 г/л? Изменением объема колбы вследствие охлаждения стекла пренебречь. Решение. Объем одного и того же количества газа согласно закону Гей-Люссака при 0°С должен быть меньше, чем при 200°С. Если при t2 = 0°С его объем V2 = 2 л, то при t1 = 200°Сон может быть определен из уравнения (1.3):
При 0°С масса газа в двухлитровой колбе равна 1,293x2=2,586 (г). При 200°С такую же массу будет иметь 3,465 л. Таким образом, если температура понизится с 200°С до 0°С, то в колбу войдет 3,465-2=1,465 (л) воздуха; соответствующая масса может быть определена из пропорции:
Следовательно, масса газа в колбе увеличится на 1,093 г. 4.Смесь эквивалентных количеств этана и кислорода находится в замкнутом сосуде при температуре 15°С и давлении 1·105 Па. Каково будет давление после взрыва смеси и приведения содержимого сосуда к первоначальной температуре? Решение. Напишем уравнение реакции горения этана: 2С2Н6 + 7О2 = 4СО2 + 6Н2О Вода при температуре 15°С будет в жидком состоянии, и при подсчета числа молекул не нужно учитывать образовавшихся молекул воды (так как объем жидкости по сравнению с объемом газа той же массы несоизмеримо мал). Из уравнения следует, что из 9 молекул исходных веществ образовалось 4 молекулы. Так как объем газов и температура остаются постоянными, то с уменьшением числа молекул в 9/4 раза и давление должно уменьшиться в такое же число раз, т.е. оно будет равно: 1·105:9/4=0,4·105 Па. 5.Для хлорирования питьевой воды хлор доставляется в баллонах под давлением. Давление в этих баллонах равно ,722·105 Па при 0°С и 15,47·105 Па при 30°С. Можно ли считать хлор в этих условиях идеальным газом? Решение. Так как в баллоне объем постоянен, то для идеального газа, как следует из уравнения (I, 5), 6. При температуре 18°С и давлении 98,64 кПа объем газа равен 2 л. Привести объем газа к равным нормальным условиям. Решение. Из уравнения (1.6) находим V1 – объем при нормальном давлении 1,013·105 Па и температуре 273 К. Данные задачи переводим в единицы СИ:
7. Вычислить при нормальных условиях газовую постоянную R, выразив ее в: а) Па·м3/(моль·К); б) Дж/(моль·К). Решение. Из уравнения (1.7) находим: а) б) 8,314 Па·м3/(моль·К) = 8,314 Н/м2 · м3/(моль·К) = 8,314 Дж/(моль·К). 8. Какое количество вещества и какая масса кислорода находится в газометре емкостью 10 л при 20°С и под давлением 100 кПа? Решение. Решаем уравнение (1.8) относительно n:
m = nM ; m = 0,41 · 32 = 13,12 (г) 9. По методу В. Майера определялась относительная молекулярная масса этилового эфира. При испарении эфира массой 0,0856 г его пары вытеснили в эвдиометрическую трубку воздух объемом 29,2 мл; высота водяного столба в эвдиометрической трубке 22,5 см, температура воздуха 17°С, атмосферное давление 1005 гПа. Давление насыщенного пара воды при 17°С равно 19,37гПа. Вычислить относительную молекулярную массу эфира и найти относительную ошибку опыта в процентах. Решение. Давление сухого воздуха, заключенного в эвдиометрической трубке, будет равно:
где 1 – значение плотности воды и 13,6 – значение плотности ртути. Подставляем в уравнение (I, 9) соответствующие значения, выразив их в единицах СИ, получаем:
Таким образом, относительная молекулярная масса эфира равна 72,94. Относительная ошибка в процентах равна: (74,08-72,94)·100:74,08-1,54 % где 74,08 – табличная величина относительной молекулярной массы эфира. 10. Смешаны водород объемом 3 л и под давлением 2·105 Па с кислородом объемом 2 л под давлением 1·105 Па. Общий объем смеси равен 4 л. Определить парциальные давления газов и общее давление смеси. Решение. Водород, занимавший объем V1, равный 3 л, при давлении p1 равном 2·105 Па, после смешивания с кислородом распространится в объеме V2, равном 4 л. Парциальное давление водорода , равное p2, находим из закона Бойля – Мариотта (1.1):
Парциальное давление кислорода находим аналогичным способом:
Общее давление p смеси равно: 1,5·105 + 0,5·105 = 2·105 (Па). 11. Смесь из 2 моль азота, 3 моль кислорода и некоторого количества вещества аммиака при 20°С и давлении 4·105 Па занимает объем 40 дм3. Вычислить количество аммиака в смеси и парциальное давление каждого из газов. Решение. Из уравнения (1.8) находим n – общее количество всех газообразных веществ, составляющих смесь, и подставляем R, равное 8,314 Дж/(моль·К), p = 4·105 Па, V = 4·10-2 м3, T =273+20 = 293 К :
Количество вещества аммиака n (NH3) = 6,57 – 2 – 3 = 1,57 (моль) Парциальное давление газов вычисляем по уравнению (1.11а): p (N2) = 4·105 · 2 : 6,57 = 1,217·105 (Па); p (O2) = 4·105 · 3 : 6,57 =1,826·105 (Па); p (NH3) = 4 · 105 · 1,57 : 6,57 =0,956·105 (Па). 12. 0,5 моль водорода и 0,25 моль азота находятся в газометре вместимостью 5 л при 10°С. Вычислить парциальное давление каждого из газов и состав смеси в объемных долях. Решение. Парциальное давление каждого компонента находим из уравнения (1.8):
По формуле (1.12) вычисляем содержание водорода и азота в объемных долях:
13. Какое давление будет иметь при 0°С кислород объемом 10 л и количеством вещества 0,25 моль? Средняя квадратичная скорость молекул кислорода при этой температуре равна 461 м/с. Решение. Из формулы (I, 13) находим давление, подставляя значения в единицах СИ: 10 л равны 0,01 м3, масса газа (N·ma) равна произведению молярной массы на количество вещества, т.е. 0,032 кг/моль · 0,25 моль = 0,008 кг:
14. При какой температуре средняя квадратичная скорость молекул хлора будет равна 500 м/с? Решение. Из формулы (1.14) находим T:
Подставляем значения, выражая их в СИ: ū в м/с, М в кг/моль, а R в Дж/(моль·К), и получаем:
Следовательно, температура t будет равна: 711,7 – 273 = 483,7 (°С)
Поиск по сайту: |


 , или
, или  (1.1)
(1.1) (1.1a)
(1.1a) (1.2)
(1.2)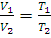 (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9)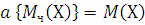
 (1.10)
(1.10) ,
,  , …,
, …,  (1.11а)
(1.11а) (1.11б)
(1.11б) , (1.13)
, (1.13) , (1.14)
, (1.14) (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17) относятся к первому газу, а ū2 и
относятся к первому газу, а ū2 и  - ко второму.
- ко второму. (1.18)
(1.18) (1.19)
(1.19) (1.20)
(1.20) , а
, а  - константа, называемая постоянной Больцмана.
- константа, называемая постоянной Больцмана.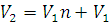

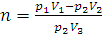

 ;
; 
 ;
; 
 ;
; 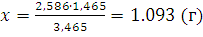
 - величина постоянная. Вычисляем это отношение для хлора: при 0°С
- величина постоянная. Вычисляем это отношение для хлора: при 0°С  , а при 30°С
, а при 30°С  . Оно непостоянно. Следовательно, хлор в этих условиях считать идеальным газом нельзя.
. Оно непостоянно. Следовательно, хлор в этих условиях считать идеальным газом нельзя. ;
; 
 . Подставляем в эту формулу числовые значения: p=1.01325·105Па, Т-273,15 К и Vm=2,2414·10-2 м3 (молярный объем газа):
. Подставляем в эту формулу числовые значения: p=1.01325·105Па, Т-273,15 К и Vm=2,2414·10-2 м3 (молярный объем газа): ;
; . Данные задач подставляем в уравнение в единицах СИ: R=8,314 Дж/(моль·К), p=1·105 Па, Т=273+20=293 К, V=0,01 м3:
. Данные задач подставляем в уравнение в единицах СИ: R=8,314 Дж/(моль·К), p=1·105 Па, Т=273+20=293 К, V=0,01 м3:


 ;
;  .
.

 ;
; 
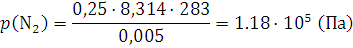
 ;
; 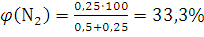
 ;
;