 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Внецентренно - сжатые колонны
Стержень сквозной колонны состоит из двух и более ветвей, связанных между собой решеткой. Сквозную колонну рассматривают как ферму с параллельными поясами, полагая, что под действием расчетных усилий M и N в ее ветвях возникают только осевые продольные силы, а поперечная сила Q воспринимается решеткой. В стержнях сквозных сечений при соединении ветвей планками и при действии поперечной силы при расчете на прочность и устойчивость учитывают дополнительный момент в плоскости, параллельной плоскости планок, и определяемый как
где Q B – перерезывающая сила в ветви ( параллельная плоскости планок); ℓ - шаг планок. При одинаковых ветвях колонны поперечная сила распределяется между ними поровну. При разных ветвях она распределяется между ними пропорционально моментам инерции ветвей относительно осей, перпендикулярных плоскости планок. При N → NКР быстро увеличиваются прогибы f, изгибающие моменты и напряжения (рис. 3.8); это приводит к потере несущей способности ( так называемой потере устойчивости второго рода). Несущая способность такой колонны может быть исчерпана в результате потери устойчивости отдельной ветви ( в плоскости или из плоскости действия момента) а также вследствие потери устойчивости колонны как единого составного стержня. Предварительный подбор сечения стержня сквозной колонны производят в следующем порядке.
e
f NКР N
Рис.3.8. Условия потери несущей способности стержня
1.Устанавливают наиболее невыгодные комбинации усилий М и N и по формуле
N уВ M
b0 b0
определяют продольные силы в ветвях. Здесь уВ – расстояние между центральными осями всего сечения колонны и отдельной ветви, противоположной рассматриваемой (рис.3.9); b0 – расстояние между центральными осями ветвей. В симметричном сечении уВ = b0 / 2 ≈ bH / 2, в асимметричном – расстояние до подкрановой ветви у2В ≈ (0,4…0,6) bH , расстояние до наружной ветви у1В ≈ (0,6…0,4) bH . 2.Задаваясь коэффициентом продольного изгиба φ = 0,7…0,9, по формуле
N в
φ R
ориентировочно находят требуемую площадь сечения каждой ветви.
      
раскос ℓВ
х2 х х1
уС у1В у2В
b 0 bH
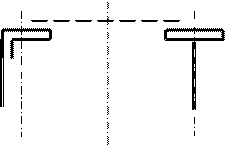
Рис.3.9. Схема нагружения ветвей стержня колонны
3.Компонуют сечения ветвей. После подбора сечения вычисляют геометрические характеристики каждой ветви в отдельности и сечения колонны в целом, необходимые для окончательной проверки на устойчивость, которую выполняют в следующей последовательности. 1.Исходя из установленного положения центра тяжести всего сечения, уточняют значения продольных усилий в ветвях. 2.По формуле
N
φ FБР
( FБР – площадь сечения всего стержня брутто) проверяют устойчивость каждой ветви как центрально-сжатого стержня. Коэффициент φ принимают по таблицам в зависимости от наибольшего из двух значений гибкости λ В и λ у. 3.Подбирают сечение элементов решетки. Раскосы рассчитывают на поперечную силу. Распорки рассчитывают на поперечную силу или исходя из предельной гибкости λПРЕД = 150. 4.По формуле
FБР
FP
( k- коэффициент, принимаемый в зависимости от угла наклона раскосов решетки (см. рис.3.9); FP – площадь сечения двух раскосов решетки ) определяют приведенную гибкость, а также условную приведенную гибкость в плоскости действия изгибающего момента МХ
E
5.Вычисляют относительный эксцентриситет
eX MX FБР уСЖ
ρX N JX
где еХ = МХ / N – эксцентриситет продольной силы относительно оси х; ρХ = WX / FБ Р – ядровое расстояние, в среднем равное 0,45 b; b- высота сечения; МХ – наибольший изгибающий момент; F Б Р – площадь всего сечения колонны; JX – момент инерции всего сечения относительно оси х; уСЖ – расстояние от центра тяжести всего сечения до центра тяжести наиболее сжатой ветви (но не менее расстояния до оси стенки ветви). 6.По таблицам в зависимости от условной приведенной гибкости и относительного эксцентриситета по СНиП II –B.3 – 72 принимают коэффициент снижения расчетного сопротивления при внецентренном сжатии φВН. 7.По формуле
N
φВН FБ Р
проверяют устойчивость колонны как единого составного стержня в плоскости действия изгибающего момента МХ. Для внецентренно растянутых элементов, когда сила приложена с эксцентриситетом е,
N N e
FНТ WНТ
При внецентренном сжатии стержня постоянного сечения по длине нагрузка также вызывает дополнительно и изгиб. Возрастание нагрузки N приводит к увеличению внешнего изгибающего момента вследствие увеличения прогиба (е + f ), где е – первоначальный эксцентриситет. Прочность внецентренно сжатого стержня проверяется по формуле
N e FНТ
FНТ WНТ
где WНТ – момент сопротивления нетто в плоскости действия изгибающего момента для сжатого волокна.
Поиск по сайту: |

 N
N






 е f
е f

 N
N




 NВ = ± (3.14)
NВ = ± (3.14) FТР = (3.15)
FТР = (3.15)


 N2В М N1В
N2В М N1В

 N
N
 α
α 
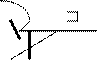






 Q
Q







 распорка
распорка

 у у
у у
























 σ = ≤ R
σ = ≤ R

 λПР = λу2 + k (3.16)
λПР = λу2 + k (3.16)
 R
R
 λХ = λХ (3.17)
λХ = λХ (3.17)

 σ = ≤ R (3.19)
σ = ≤ R (3.19)
 σ = + . (3.20)
σ = + . (3.20)



 σ = 1 + ≤ m K R, (3.21)
σ = 1 + ≤ m K R, (3.21)