 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение изгибающих моментов в сечениях вала ⇐ ПредыдущаяСтр 7 из 7
Составляем (рис. 11) расчетную схему вала в соответствии с рекомендациями п. 5.2, и рис. П5: 1. Строим кинематическую схему редуктора. Выбираем систему координат: xoz – горизонтальная плоскость, yoz – вертикальная. 2. Выбираем направление вращения быстроходного вала редуктора по часовой стрелке. 3. Выбираем направление винтовой линии зубьев шестерни левое, чтобы уменьшить суммарную внешнюю осевую силу 4. Определяем по формулам рис. П5 силы в зацеплениях: Быстроходная передача: 1) Окружная сила шестерни и колеса
2) Радиальная сила шестерни и осевая сила колеса
3) Осевая сила шестерни и радиальная сила колеса
Тихоходная передача: 1) Окружная сила шестерни и колеса
2) Радиальная сила шестерни и радиальная сила колеса
3) Осевая сила шестерни и радиальная сила колеса
5. Строим (рис. 11) схему нагружения валов. Направление сил в зацеплениях определяем в соответствии с выбранными направлениями вин-
товой линии зубьев колес и вращения валов. 6. Строим (рис. 11) расчетную схему промежуточного вала. 7. Определяем линейные расстояния между точками приложения радиальных сил в зацеплениях и реакций в опорах: а) по формуле (3) рассчитываем расстояние а точки приложения радиальной реакции для выбранных роликовых конических подшипников
б) по формулам рис. П5 рассчитываем линейные расстояния l:
где ВП=Т – ширина подшипника: x=8 мм – зазор. 8. Для двух плоскостей XOZ и YOZ строим расчетные схемы вала, где показываем силы, действующие в зацеплениях и реакции в опорах (направление реакций принимаем предварительно).
Определение реакций в опорах В горизонтальной плоскости XOZ:
в) В вертикальной плоскости YOZ: a)
б)
в)
Определение изгибающих и крутящих моментов В сечениях вала Значения моментов определяем для характерных сечений вала (рис. 11). В горизонтальной плоскости XOZ: Сечение А: МXА=0; Сечение В: МXВ=0; Сечение Е слева: Сечение Е справа:
Сечение С слева:
Сечение С справа: Сечение Р:
В вертикальной плоскости YOZ: Сечение А: МYА=0; Сечение В: МYВ=0; Сечение Е: МYE=-RAY×l1=-4354×45=-195930 Н×мм; Сечение С: МYC=-RBY×l3=-2839×46=-130594 Н×мм; Сечение Р:
Крутящий момент МК передается вдоль оси вала, а т.к. редуктор с одним потоком мощности, то величина МК в разных сечениях постоянна и совпадает со значением вращающего момента промежуточного вала:
На основании полученных значений изгибающих МХ, МY и крутящего МК моментов строим (рис. 11) эпюры. Для проведения прочностных расчетов выделяем предположительно два наиболее опасных сечения вала: 1. Сечение С-С под колесом быстроходного колеса, здесь источниками концентрации напряжений являются шпоночная канавка и натяг от посадки колеса; 2. Сечение Р-Р на торце шестерни тихоходной передачи со стороны буртика колеса, здесь источником концентрации напряжений является ступенчатое изменение вала с галтельным переходом. Сечение Е-Е не будем рассматривать, т.к. зубья шестерни выполнены заодно с валом и Суммарные изгибающие моменты в опасных сечениях:
Поиск по сайту: |
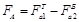 вала.
вала. ;
; Н;
Н;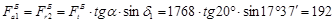 Н;
Н; Н;
Н;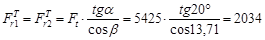 Н;
Н; Н;
Н;
 мм
мм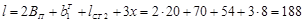 мм;
мм;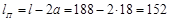 мм;
мм; мм;
мм; мм;
мм; мм;
мм;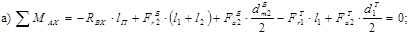

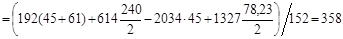 Н.
Н.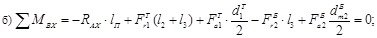
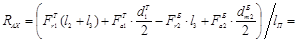
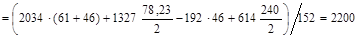 Н.
Н.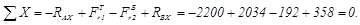


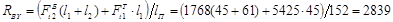 Н.
Н.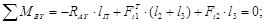
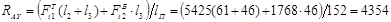 Н.
Н.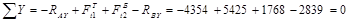 .
.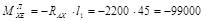 Н×мм;
Н×мм;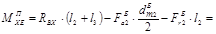
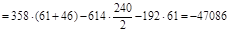 Н×мм;
Н×мм;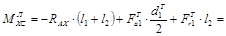
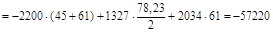 Н×мм;
Н×мм; Н×мм;
Н×мм;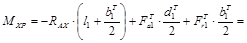
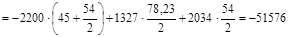 Н×мм.
Н×мм.
 Н×мм.
Н×мм.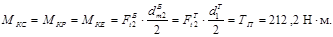
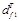 >dБК, запас прочности в этом сечении будет обеспечен.
>dБК, запас прочности в этом сечении будет обеспечен. Н×мм;
Н×мм; Н×мм.
Н×мм.