 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Нелінійне програмуванняСтр 1 из 3Следующая ⇒
Кременчуцький державний політехнічний УНІВЕРСИТЕТ
МЕТОДИЧНІ ВКАЗІВКИ ЩОДО ПРОВЕДЕННЯ ЛАБОРАТОРНОЇ РОБОТИ З НАВЧАЛЬНОЇ ДИСЦИПЛІНИ “МАТЕМАТИЧНЕ ПРОГРАМУВАННЯ” З ТЕМИ “НЕЛІНІЙНЕ ПРОГРАМУВАННЯ. КВАДРАТИЧНЕ ПРОГРАМУВАННЯ” ДЛЯ СТУДЕНТІВ ДЕННОЇ ТА ЗАОЧНОЇ ФОРМ НАВЧАННЯ З УСІХ СПЕЦІАЛЬНОСТЕЙ ФАКУЛЬТЕТІВ ЕКОНОМІЧНОГО ТА УПРАВЛІННЯ
КРЕМЕНЧУК 2006
Методичні вказівки щодо проведення лабораторної роботи з навчальної дисципліни “Математичне програмування” з теми “Нелінійне програмування. Квадратичне програмування ” для студентів денної та заочної форм навчання з усіх спеціальностей факультетів економічного та управління
Укладач доцент В.Є. Черніченко
Рецензент О.І. Маслак
Кафедра економіки
Затверджено методичною радою КДПУ
Протокол № від "___" ________________ 2006р.
Голова методичної ради проф. В.В. Костін
Кременчук 2006 Зміст
1. Мета лабораторної роботи по темі “Нелінійне програмування. Квадратичне програмування ”
Метою даної лабораторної роботи є розв’язання задачі квадратичного програмування на основі ознайомлення з основними теоретичними положеннями за даною тематикою. Для виконання лабораторної роботи студент повинен знати: - мету і зміст заданої роботи, порядок її виконання; - основні теоретичні положення з тематики “Нелінійне програмування. Квадратичне програмування ”; - алгоритм розв’язання задачі; Студент повинен уміти: - користуватися пакетом MS Excel; - будувати область допустимих розв’язків на графіці; - згорнути квадратичну форму до рівняння кола. Студент повинен підготувати: - алгоритм виконання лабораторної роботи з використанням таблиць Excel.
2 Зміст теоретичних положень з теми “Нелінійне програмування. Квадратичне програмування ” Нелінійне програмування Загальне завдання нелінійного програмування Часто зустрічаються завдання математичного програмування, коли або функція мети, або обмеження нелінійні. Такого типу завдання називаються завданнями нелінійного програмування. Загальний вигляд цих завдань:
Причому, хоча б одна з функцій Приклад 2.1
Складність розв’язання задач нелінійного програмування. 1. Область допустимих рішень, що задається обмеженнями (2.2) може бути не опукла. 2. Мінімум або максимум функції мети може досягатися не в крайніх точках, а всередині області допустимих розв’язків. Тому немає загальних методів розв’язання задач нелінійного програмування. Далі розглядатиметься розв’язання задач опуклого програмування. Опуклі функції Функція
Функція опукла на відрізку, якщо для будь-якої внутрішньої точки цього відрізка, виконуватиметься нерівність (2.3), тобто точки графіка функції f лежатимуть вище за точки відрізка, що сполучає точки кінців графіка. Для того, того щоб область допустимих рішень була опукла, необхідно щоб кожна нерівність (2.2) задавала опуклу область, а це можливо тільки у разі опуклості функції qi.
Множина опукла, якщо воно містить відрізок, що сполучає дві будь-які його точки. Покажемо, що множина, яка задається нерівністю (2.4), випукле. Не хай
Покажемо, що і точка Через опуклість
Тоді, враховуючи (2.5), отримаємо
Таким чином, одержали, що і точка Під час розв’язання задач опуклого програмування використовується Куна — Таккера. Не хай дане завдання нелінійного програмування: I знайти максимальне значення функції при обмеженнях
Складемо функцію Лагранжа для даного завдання:
Якщо виконується умова регулярності, існує принаймні одна точка X, для якої
Теорема. Вектор
Точка
Поиск по сайту: |



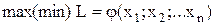 , (2.1)
, (2.1)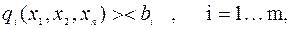 (2.2)
(2.2) - без обмеження.
- без обмеження. - нелінійна.
- нелінійна.

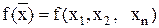 - опукла, якщо виконується
- опукла, якщо виконується (2.3)
(2.3)
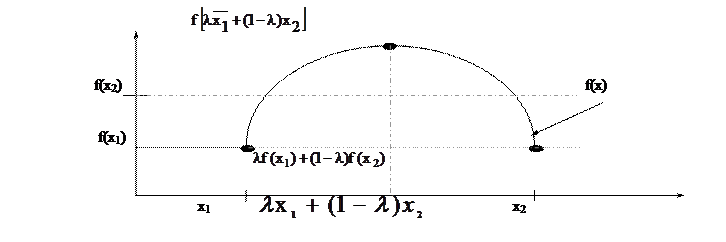 Рис2.1 Геометрическая ілюстрація опуклої функції
Рис2.1 Геометрическая ілюстрація опуклої функції i=1,.,m (2.4)
i=1,.,m (2.4)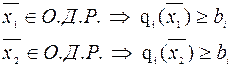 i=1,...m (2.5) тобто точки х1 і х2 належать області допустимих рішень, (О.Д.Р.)
i=1,...m (2.5) тобто точки х1 і х2 належать області допустимих рішень, (О.Д.Р.) =
=  теж належить О.Д.Р.
теж належить О.Д.Р.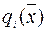 виконується (2.6)
виконується (2.6) ,i=1...m (2.6)
,i=1...m (2.6) i=1,...m (2.7)
i=1,...m (2.7)
 (2.8)
(2.8)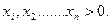
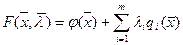 (2.9)
(2.9)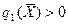 (для всіх i) l, то має місце наступна теорема.
(для всіх i) l, то має місце наступна теорема. тоді й тільки тоді є - оптимальним розв’язком задачі (2.8), коли існує такий вектор
тоді й тільки тоді є - оптимальним розв’язком задачі (2.8), коли існує такий вектор 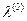 , що при
, що при 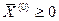 і
і 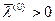 для всіх
для всіх 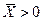 і
і 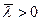 .
. .
.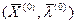 називається сідлової точкою для функції
називається сідлової точкою для функції  , а теорема називається теоремою про сідловой точку.
, а теорема називається теоремою про сідловой точку.