 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Оптимизационные задачи для выпуклых функций
Общим недостатком рассмотренных выше методов безусловной оптимизации было, с одной стороны, то, что они позволяют отыскивать только точки возможного локального экстремума, а с другой - то, что найденные решения могут существенно зависеть от начального приближения. Поиск глобального оптимума подразумевает перебор найденных точек, который, в случае градиентных методов, может быть осуществлен за счет подбора соответствующих начальных приближений
Рис. 2.1
Рис. 2.2
Однако существует один класс функций, для которых градиентные методы приводят к нахождению глобального оптимума. Это выпуклые функции. Определение. Функция
если же
то функция называется вогнутой. Геометрический смысл понятий выпуклости и вогнутости для случая функции одной переменной представлен на Рис. 2.3. Из него, в частности, видно, что график выпуклой функции лежит ниже отрезка, соединяющего точки
Рис. 2.3
Можно доказать, что достаточным условием выпуклости функции
называемой также матрицей Гессе, во всех точках Как следует из геометрической интерпретации, для выпуклой функции локальный экстремум, если он существует, совпадает с глобальным. Справедлива теорема. Теорема 2.2. Если Доказательство.Доказательство достаточно провести для случая вогнутой функции, т. к. для противоположного случая оно будет аналогичным с точностью до знака. Пусть
откуда следует
Если ввести вектор
Устремляя
По условию теоремы
Следовательно, для любой точки х отличной от Поскольку выпуклые функции обладают столь «полезными» оптимизационными качествами, они занимают исключительно важное место в теории исследования операций. Соответствующий раздел математического программирования получил название выпуклого программирования, а общая задача выпуклого программирования формулируется как проблема поиска максимума вогнутой (минимума выпуклой) функции на выпуклом множестве.
Поиск по сайту: |
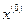 .
.

 называется выпуклойв области D, если для любых двух точек
называется выпуклойв области D, если для любых двух точек 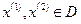 и любого
и любого  выполняется неравенство
выполняется неравенство (14)
(14) (15)
(15) и
и  , а график вогнутой - выше этого отрезка.
, а график вогнутой - выше этого отрезка.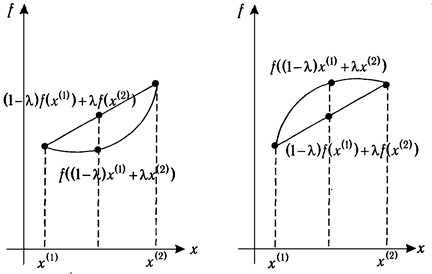
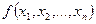 является положительная определенность матрицы
является положительная определенность матрицы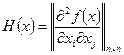
 . Соответственно, достаточным условием вогнутости является отрицательная определенность матрицы Гессе. В частности, для функций одной переменной достаточным условием выпуклости (вогнутости) является выполнение неравенства
. Соответственно, достаточным условием вогнутости является отрицательная определенность матрицы Гессе. В частности, для функций одной переменной достаточным условием выпуклости (вогнутости) является выполнение неравенства 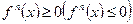 .
. выпуклая (вогнутая) на
выпуклая (вогнутая) на  функция и
функция и 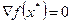 , то
, то 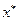 - точка глобального минимума (максимума)
- точка глобального минимума (максимума) - произвольная точка, отличная от точки
- произвольная точка, отличная от точки 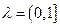 , в силу вогнутости функции
, в силу вогнутости функции 
 .
. и обозначить
и обозначить 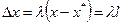 , то длина вектора
, то длина вектора  будет равна
будет равна 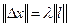 . Следовательно,
. Следовательно, .
. и учитывая, что вектор l сонаправлен с
и учитывая, что вектор l сонаправлен с  .
. .
. , т.е.
, т.е.