 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Постановка задачи нелинейного программированияСтр 1 из 6Следующая ⇒
Глава 3. Нелинейное программирование.
Предположение о возможности описать зависимости между управляемыми переменными с помощью линейных функций вообще говоря не всегда адекватно природе моделируемого объекта. Например, в рассмотренных моделях цена товара считается независимой от количества произведенного продукта, однако в повседневной жизни мы постоянно сталкиваемся с тем, что она может зависеть от объема партии товара. Аналогичные замечания могут быть сделаны и по поводу технологических ограничений: расход определенных видов сырья и ресурсов происходит не линейно, а скачкообразно (в зависимости от объема производства). Попытки учесть эти факторы приводят к формулировке более общих и сложных оптимизационных задач. Изучение методов их решения составляет предмет научной области, получившей названия нелинейного программирования. Общая задача нелинейного программирования (ОЗНП) определяется как задача нахождения максимума (или минимума) целевой функции
где хотя бы одна из функций f или По аналогии с линейным программированием ЗНП однозначно определяется парой
Для определенности, в дальнейшем по умолчанию будем рассматривать задачи максимизации. Как и в ЗЛП, вектор С точки зрения экономической интерпретации Задача (2) является общей, т. к. допускает запись логических условий, например:
или запись условий дискретности множеств:
Набор ограничений, определяющих множество D, при необходимости всегда можно свести либо к системе, состоящей из одних неравенств: либо, добавив фиктивные переменные у, к системе уравнений:
Перечислим свойства ЗНП, которые существенно усложняют процесс их решения по сравнению с задачами линейного программирования: 1. Множество допустимых планов D может иметь очень сложную структуру (например, быть невыпуклым или несвязным). 2. Глобальный максимум (минимум) может достигаться как внутри множества D, так и на его границах (где он, вообще говоря, будет не совпадать ни с одним из локальных экстремумов). 3. Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа. В силу названных факторов задачи нелинейного программирования настолько разнообразны, что для них не существует общего метода решения.
Поиск по сайту: |
 на множестве D, определяемом системой ограничений
на множестве D, определяемом системой ограничений (1)
(1)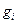 является нелинейной.
является нелинейной. и кратко может быть записана в следующем виде
и кратко может быть записана в следующем виде
 называется допустимым планом, а если для любого
называется допустимым планом, а если для любого  выполняется неравенство
выполняется неравенство  , то
, то 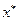 называют оптимальным планом. В этом случае
называют оптимальным планом. В этом случае  может рассматриваться как доход, который получает фирма (предприятие) при плане выпуска х, а
может рассматриваться как доход, который получает фирма (предприятие) при плане выпуска х, а  как технологические ограничения на возможности выпуска продукции. В данном случае они являются обобщением ресурсных ограничений в ЗЛП
как технологические ограничения на возможности выпуска продукции. В данном случае они являются обобщением ресурсных ограничений в ЗЛП 

 .
.
