 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методы поиска экстремума функции
Одним из наиболее общих подходов к решению задачи поиска экстремума (локального максимума или минимума) функции при наличии связующих ограничений на ее переменные (или, как еще говорят, задачи условной оптимизации) является метод Лагранжа.Идея метода состоит в сведении задачи поиска условного экстремума целевой функции
на множестве допустимых значения D, описываемом системой уравнений к задаче безусловной оптимизации функции
где Теорема 2.1.Если
равен т, то существуют такие
Из теоремы (1) вытекает метод поиска условного экстремума, получивший название метода множителей Лагранжа, или просто метода Лагранжа.Он состоит из следующих этапов. 1. Составление функции Лагранжа 2. Нахождение частных производных
3. Решение системы уравнений
относительно переменных х и и. 4. Исследование точек, удовлетворяющих системе (7), на максимум (минимум) с помощью достаточного признака экстремума. Наличие четвертого этапа объясняется тем, что теорема (1) дает необходимое, но не достаточное условие экстремума. Проверка достаточных условий экстремума сопряжена со значительными трудностями. Основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить множество доступных средств решения задачи. Заметим, что задача решения системы уравнений (7), к которой сводится данный метод, в общем случае не проще исходной проблемы поиска экстремума (3)-(4). Методы, подразумевающие такое решение, называются непрямыми. Они могут быть применены для весьма узкого класса задач, для которых удается получить линейную или сводящуюся к линейной систему уравнений (7). Их применение объясняется необходимостью получить решение экстремальной задачи в аналитической форме (допустим, для тех или иных теоретических выкладок). При решении конкретных практических задач обычно используются прямые методы, основанные на итеративных процессах вычисления и сравнения значений оптимизируемых функций. Ведущее место среди прямых методов решения экстремальных задач занимает градиентный метод (точнее, семейство градиентных методов) поиска стационарных точек дифференцируемой функции. Стационарной называется точка, в которой Идея данного метода основана на том, что градиент функции указывает направление ее наиболее быстрого возрастания в окрестности той точки, в которой он вычислен. Поэтому, если из некоторой текущей точки Однако одновременно с определением направления сдвига возникает вопрос о величине этого сдвига или, другими словами, возникает проблема выбора шага l, в рекуррентной формуле
задающей последовательность точек, стремящихся к точке максимума. В зависимости от способа ее решения различают различные варианты градиентного метода. Рассмотрим наиболее известных из них.
Поиск по сайту: |
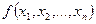 (3)
(3)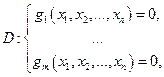 (4)
(4)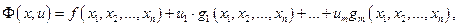 (5)
(5) - вектор дополнительных переменных, называемых множителями Лагранжа. Функцию
- вектор дополнительных переменных, называемых множителями Лагранжа. Функцию  , где
, где 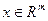 ,
, 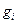 справедлива теорема, определяющая необходимое условие существования точки условного экстремума в задаче (3)-(4).
справедлива теорема, определяющая необходимое условие существования точки условного экстремума в задаче (3)-(4).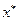 - точка условного экстремума функции (3) при ограничениях (4) и ранг матрицы первых частных производных функций
- точка условного экстремума функции (3) при ограничениях (4) и ранг матрицы первых частных производных функций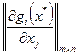
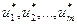 , не равные одновременно нулю, при которых
, не равные одновременно нулю, при которых . (6)
. (6)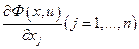 и
и  /
/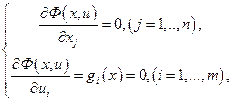 (7)
(7)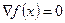 и в которой, в соответствии с необходимым условием оптимальности, возможно достигается локальный экстремумум. Таким образом, применяя градиентный метод, находят множество точек локальных максимумов (или минимумов), среди которых определяется глобальный максимум (или минимум).
и в которой, в соответствии с необходимым условием оптимальности, возможно достигается локальный экстремумум. Таким образом, применяя градиентный метод, находят множество точек локальных максимумов (или минимумов), среди которых определяется глобальный максимум (или минимум). перемещаться в направлении вектора
перемещаться в направлении вектора 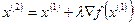 ,
, 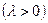 , лежащей в такой окрестности, справедливо неравенство
, лежащей в такой окрестности, справедливо неравенство  . Продолжая этот процесс, мы постепенно будем приближаться к точке некоторого локального максимума (см. Рис. 2.1).
. Продолжая этот процесс, мы постепенно будем приближаться к точке некоторого локального максимума (см. Рис. 2.1).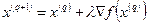 , (8)
, (8)