 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производная неявной функции
Если неявная функция задана уравнением
Пример Найти производную функции:
Логарифмическое дифференцирование В ряде случаев, когда приходится дифференцировать произведение многих сомножителей или частное, в котором и числитель и знаменатель состоят из нескольких сомножителей, а также при нахождении производных от показательно-степенной функции Метод логарифмического дифференцирования заключается в том, что от заданной функции у сначала находится натуральный логарифм, а затем результат дифференцируется:
Из полученного равенства определяется
Примеры Найти производные функций: 1.
2.
Производные высших порядков Производная Производную от первой производной называют производной второго порядка или второй производной и обозначают Итак, по определению
Вторая производная играет роль ускорения изменения функции. Производная от производной второго порядка называется производной третьего порядка и обозначается Таким образом,
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
Число n, указывающее порядок производной, заключают в скобки, чтобы не путать с показателем степени. Производные порядка выше первого называются производными высших порядков. Порядок производной, начиная с четвертого, обозначают римскими цифрами или арабскими цифрами в скобках, например,
Примеры 1. Найти
2. Найти
Определение дифференциала функции С понятием производной тесно связано понятие дифференциала функции. Пусть функция
Определение. Дифференциалом функции
Для функции
Тогда
Значит, дифференциал функции равен произведению ее производной на дифференциал независимой переменной. Из формулы
Следовательно, производная функции равна отношению дифференциала функции к дифференциалу ее аргумента.
Поиск по сайту: |
 , то для нахождения производной от у по х надо продифференцировать это уравнение по х, рассматривая при этом у как функцию от х, и затем, полученное уравнение разрешить относительно
, то для нахождения производной от у по х надо продифференцировать это уравнение по х, рассматривая при этом у как функцию от х, и затем, полученное уравнение разрешить относительно 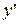 , выразив
, выразив  .
.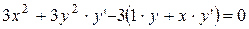 ;
; ;
; ;
; .
. , применяют логарифмическое дифференцирование.
, применяют логарифмическое дифференцирование. .
. .
. .
. ;
; ;
; ;
; ;
; .
.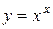 .
.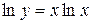 ;
; ;
; ;
; .
. от функции
от функции  называется производной первого порядка (или первой производной) и представляет собой функцию от х.
называется производной первого порядка (или первой производной) и представляет собой функцию от х.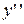 ,
, 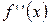 ,
,  .
.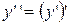 .
. ,
,  ,
,  .
. .
. .
. или
или  и т.д.
и т.д. .
. ;
; .
. для функции
для функции  .
. ;
;  ;
;  ;
; 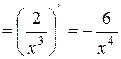 .
. или
или  .
. имеем:
имеем: , т.е.
, т.е. 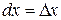 .
. или
или  .
. или
или 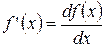 .
.