 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производная суммы, разности, произведения и частного функций
Нахождение производной функции непосредственно по определению (п.4.1) часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.
Теорема. Если функции
Следствия 1. 2. Если 3.
Производная сложной функции Пусть
Теорема. Если функции
Кратко это можно сформулировать так (правило цепочки): производная сложной функции равна произведению производных от функций ее составляющих. Данное правило распространяется на сложные функции при любом (определенном) числе промежуточных аргументов. Так, если
Производная обратной функции Если
т.е. производная обратной функции равна обратной величине производной данной функции.
Записывают:
Пример Найти производную функции
Итак,
Таблица производных Для удобства и упрощения процесса дифференцирования формулы производных основных элементарных функций и правила дифференцирования сведены в таблицу.
Примеры отыскания производных сложных функций На практике чаще всего приходится находить производные от сложных функций. Покажем на примерах, как находить производные от таких функций.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Для случая дифференцирования сложных функций, таблицу производных можно переписать в более общем виде.
Формулы дифференцирования основных элементарных функций от промежуточного аргумента
Производная функции, заданной параметрически Зависимость между переменными х и y может быть задана параметрически в виде двух уравнений:
где t − вспомогательная переменная (параметр). Функцию По правилу дифференцирования сложной функции имеем:
Так как
Примеры Найти производные функций: 1.
2.
Поиск по сайту: |
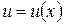 и
и  дифференцируемы в точке х, то в этой точке дифференцируемы функции
дифференцируемы в точке х, то в этой точке дифференцируемы функции  ,
, 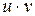 ,
, 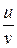 (при условии, что
(при условии, что  ) и при этом
) и при этом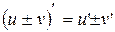 ;
;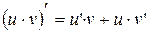 ;
;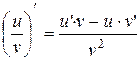 ,
, 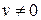 .
.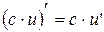 , где
, где 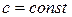 .
.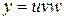 , то
, то 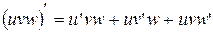 .
.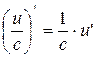 , где
, где  и
и  , тогда
, тогда  − сложная функция с промежуточным аргументом u и независимым аргументом х.
− сложная функция с промежуточным аргументом u и независимым аргументом х.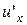 в точке х, а функция
в точке х, а функция 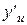 в соответствующей точке
в соответствующей точке 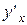 , которая находится по формуле:
, которая находится по формуле: или
или  .
.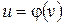 ,
, 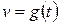 ,
, 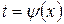 , то
, то .
. и
и 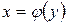 − взаимо-обратные дифференцируемые функции и
− взаимо-обратные дифференцируемые функции и 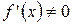 , то
, то или
или  ,
,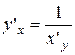 или
или  .
.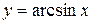 .
. , тогда
, тогда 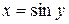 ,
,  . Имеем
. Имеем  .
. .
. .
.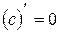 ,
, 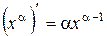
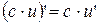 ,
, 
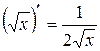
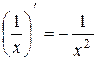
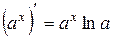


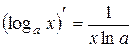


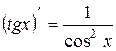


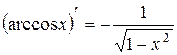
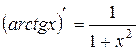
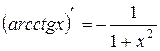
 , k − число.
, k − число. ;
;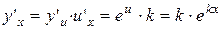 .
. .
.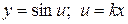 ;
;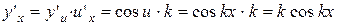 .
. .
.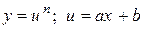 ;
;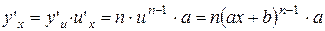 .
. .
.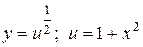 ;
;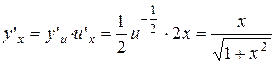 .
.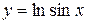 .
. ;
;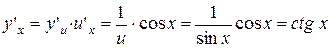 .
. .
. ;
;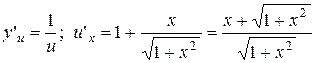 ;
; .
. .
. .
. .
.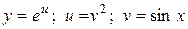 ;
;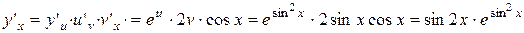 .
. .
.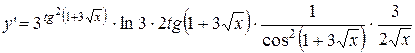 .
.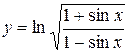 .
. ;
;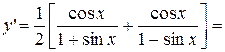
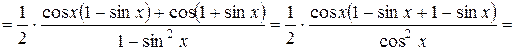
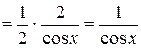 .
.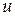 (
( 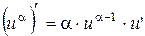

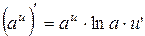

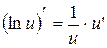
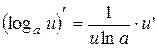
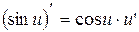
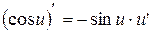
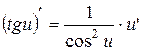
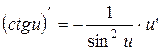

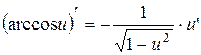

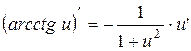
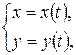
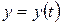 , где
, где 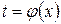 .
. .
.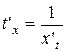 , то
, то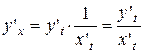 .
.
 .
.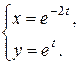
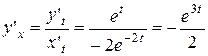 .
.