 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Физический смысл производнойСтр 1 из 4Следующая ⇒
ГЛАВА 4 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ Раздел математики, в котором изучается понятие производной и дифференциала функции, а также способы их применения к исследованию функций, называют дифференциальным исчислением.
Определение производной К понятию производной приходят при изучении скорости изменения функции. Пусть функция Проведем следующие операции: − аргументу − найдем соответствующее приращение функции:
− составим отношение:
− найдем предел этого отношения при
Если этот предел существует, то его называют производной функции
Определение. Производной функции
Записывают:
Производная функции
Определение. Операция нахождения производной функции называется дифференцированием.
Определение. Функция, имеющая производную в каждой точке интервала
Примеры 1. Найти производную функции 1)
2)
3)
4)
2. Найти производную функции 1)
2)
3)
Геометрический смысл производной Рассмотрим график функции
Рис. 4.1
Из
Пусть
Определение. Касательной к кривой
Значит, при
Следовательно,
Таким образом, геометрический смысл производной состоит в том, что значение производной равно тангенсу угла, образованного касательной к графику функции Отметим, что понятие производной дает возможность написать уравнение касательной к графику функции. Уравнение касательной − это уравнение прямой, проходящей через заданную точку: Следовательно, уравнение касательной будет
или
Если касательную к кривой в некоторой точке провести невозможно, то это означает, что функция недифферинцируема в этой точке.
Физический смысл производной Рассмотрим функцию, аргументом которой является время t. Если функция − пройденный путь
представляет собой среднюю скорость движения за промежуток времени
есть скорость движения в момент времени t или мгновенная скорость движения. В общем случае, если функция
Таким образом, производная
4.4. Зависимость между непрерывностью Сформулируем необходимое условие существования производной.
Теорема. Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна.
Заметим, что обратное утверждение неверно: непрерывная функция может не иметь производной. Например, функция Таким образом, непрерывность функции необходимое, но не достаточное условие дифференцируемости функции.
Поиск по сайту: |
 определена и непрерывна на некотором интервале
определена и непрерывна на некотором интервале 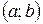 .
. дадим приращение
дадим приращение  , такое что
, такое что  ;
; ;
; ;
; :
: .
.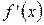 ,
,  ,
, 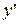 ,
, 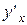 ,
,  .
. называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. или
или  .
. есть некоторая функция
есть некоторая функция 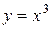 .
. ;
;
 ;
; ;
; ;
; .
. .
. ;
;
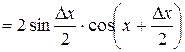 ;
; ;
;
 ;
; .
.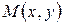 . Если аргументу х дать приращение
. Если аргументу х дать приращение 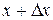 будет соответствовать точка
будет соответствовать точка  . Проведем через точки М и
. Проведем через точки М и  секущую и пусть φ − угол, который секущая М
секущую и пусть φ − угол, который секущая М 
 получаем
получаем .
.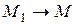 , а секущая М
, а секущая М  , где
, где  − угол наклона касательной МТ к оси Ох. Тогда
− угол наклона касательной МТ к оси Ох. Тогда .
. .
. , угловой коэффициент которой равен
, угловой коэффициент которой равен 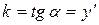 .
.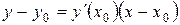
 .
. , тогда отношение
, тогда отношение
 . Предел этого отношения (производная по определению)
. Предел этого отношения (производная по определению)
 − мгновенная скорость изменения у.
− мгновенная скорость изменения у.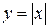 непрерывна при
непрерывна при  , но не дифференцируема для этого значения, так как в точке
, но не дифференцируема для этого значения, так как в точке