 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Радиусы кривизны земного эллипсоида
Плоскости секущие эллипсоид вращения по различным направлениям, образуют в пересечении с его поверхностью или окружности или эллипсы. Основными сечениями эллипсоида являются (рис. 1.5): - сечение плоскостью, проходящей через малую ось; - сечение плоскостью, перпендикулярной малой оси; - нормальное сечение. Сечение плоскостью, проходящей через малую ось РР¢ эллипсоида, образует на его поверхности меридианный эллипс или истинный меридиан «PQP¢Q¢». Кривизна его – переменная величина (радиус кривизны М – тоже). Радиус М уменьшается с уменьшением географической широты (j) и вычисляется по формуле:
где а – большая полуось; е – эксцентриситет Приняв, что
Рис.1.5. Радиусы кривизны земного эллипсоида
Экваториальный радиус кривизны меридиана при j = 0°: М0 = 6 335 552,6 м. Сечение эллипсоида плоскостью перпендикулярной его малой оси РР¢ дает на его поверхности малый круг qq¢ – параллель. Радиус параллели r вычисляется по формуле:
При j = 0° радиус параллели равен большой полуоси а эллипсоида, и эта параллель – земной экватор. Нормальное сечение – сечение эллипсоида плоскостью, проходящей через нормаль к его поверхности. Из бесчисленного множества возможных нормальных сечений выделяют два главных нормальных сечения – меридианное и перпендикулярное ему – сечение первого вертикала. Для сечения первого вертикала радиус кривизны эллипса N, вычисляется по формуле:
на полюсе M = N, M < N; на экваторе N0 = a. Экваториальный радиус кривизны первого вертикала при j = 0°: N0 = a = 6 378 245 м. Радиус кривизны нормального сечения, составляющего с меридианом в заданной точке угол А, вычисляется по формуле:
где М и N – величины, определяемые в зависимости от широты j по формулам (1.4) и (1.7). Радиусом средней кривизны эллипсоида в данной точке с широтой j называют среднее геометрическое из радиуса М и N. Радиус средней кривизны эллипсоида вычисляется по формуле:
Значения М, N, R даны в картографических таблицах УГС через каждые 30¢ j. Произведение любого радиуса кривизны на «arс 1¢»равно длине дуги в 1¢данного сечения. Учтя приведенные выше формулы, получим выражение для определения длин дуг: 1) – одной минуты параллели:
или без учета сжатия Земли (е = 0)
2) – одной минуты первого вертикала:
или приближенно:
3) – одной минуты меридиана:
или приближенно:
Таким образом, поверхность земного эллипсоида имеет кривизну, изменяющуюся от точки к точке по широте и от направления в данной точке. Выводы 1. Для решения задач судовождения Земной шар принимается за эллипсоид вращения с элементами референц-эллипсоида Красовского. 2. Положение точки на земной поверхности определяется географическими координатами: - географической широтой (j); - географической долготой (l). 3. Величинами, характеризующими изменение географических координат при переходе судна от одной точки к другой, являются: - разность широт (Dj, РШ) и - разность долгот (Dl, РД). 4. Форма и размеры земного эллипсоида характеризуются радиусами кривизны его основных сечений (М, r, N, rA, R).
Примечание: Самоконтроль знаний по теме проводится по тестовым заданиям к главе на базе приложения «Компьютерная система тестирования знаний «OPENTEST»».
Поиск по сайту: |
 (1.4)
(1.4)
 , то
, то (1.5)
(1.5)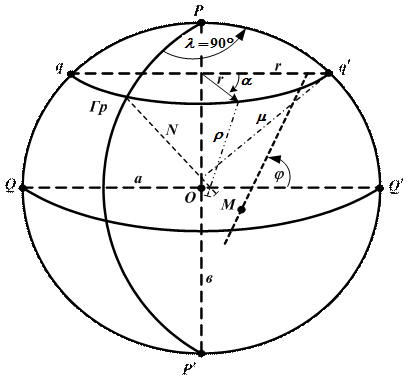
 или
или  или
или  . (1.6)
. (1.6) или
или  (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) . (1.15)
. (1.15)