 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Раскрытие неопределенностей по правилу Лопиталя
Правило Лопиталя применяется для раскрытия неопределенностей
При этом предполагается, что функции Если же отношение производных также будет представлять случай Если имеются неопределенности типа Нахождение предела функции в случае неопределенностей вида
Решение типовых примеров задания 5 РГР Найти пределы, используя правило Лопиталя. Сравнить результаты с решениями задания 1. 1. Решение. Неопределенность вида
2. Решение.
3. Решение.
= 4. Решение.
5. Решение.
6. Решение. Неопределенностьвида
Отсюда Ответы совпадают с результатами решения примеров задания 1.
2.7. Геометрический смысл производной
определена в интервале Проведем через точки Если существует предел Из
Существование конечного предела в уравнении (1.8) эквивалентно существованию конечной производной. Угловой коэффициент касательной к кривой
В этом заключается геометрический смысл производной. Найдем уравнение касательной. Из аналитической геометрии известно, что, если прямая проходит через точку Учитывая, что Уравнение (2.5) называется уравнением касательной к кривой Нормалью к кривой называется прямая, проходящая через точку касания, перпендикулярно к касательной. Поскольку угловые коэффициенты касательной и нормали связаны между собой условием перпендикулярности, то уравнение нормали к кривой
Поиск по сайту: |
 и
и  . Если при
. Если при  функции
функции  и
и  одновременно стремятся к
одновременно стремятся к  или
или  , то предел отношения равен пределу отношения их производных, т.е.
, то предел отношения равен пределу отношения их производных, т.е. .
. и
и  существуют и конечны.
существуют и конечны. , можно снова и снова применять правило Лопиталя.
, можно снова и снова применять правило Лопиталя. или
или  , то сначала приводят эти функции к виду дроби, которая представляет неопределенность
, то сначала приводят эти функции к виду дроби, которая представляет неопределенность  ,
,  ,
,  с помощью логарифмирования также сводится сначала к случаям
с помощью логарифмирования также сводится сначала к случаям 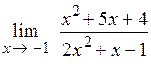 .
. .
. . Неопределенность вида
. Неопределенность вида 
 .
. . Неопределенность вида
. Неопределенность вида 
 .
. . Неопределенностьвида
. Неопределенностьвида  .
.

 .
. . Неопределенностьвида
. Неопределенностьвида  .
. .
. .
. . Прологарифмируем данную функцию сведем неопределенность к виду
. Прологарифмируем данную функцию сведем неопределенность к виду  и применим правило Лопиталя
и применим правило Лопиталя ;
; 



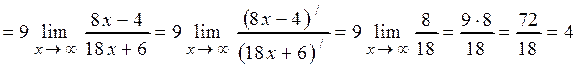 .
. ;
; 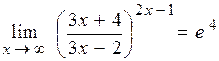 .
. Пусть функция
Пусть функция 
 и пусть точка
и пусть точка  на графике функции соответствует значе-нию аргумента
на графике функции соответствует значе-нию аргумента  , а точка
, а точка  значению
значению  (рис. 2.1).
(рис. 2.1). и
и  секущую. Обозначим через
секущую. Обозначим через  угол между секущей и осью
угол между секущей и осью  . Очевидно, этот угол зависит от
. Очевидно, этот угол зависит от  .
. , то прямую с угловым коэффициентом
, то прямую с угловым коэффициентом  , проходящую через точку
, проходящую через точку  при
при  .
. находим
находим . (2.2)
. (2.2) в точке
в точке  или тангенс угла
или тангенс угла  ,который образует касательная к кривой в данной точке с положительным направлением оси
,который образует касательная к кривой в данной точке с положительным направлением оси  , - это производная
, - это производная  в этой точке.
в этой точке. . (2.3)
. (2.3) в направлении, которое определяется угловым коэффициентом
в направлении, которое определяется угловым коэффициентом  , то уравнение этой прямой можно записать в виде
, то уравнение этой прямой можно записать в виде . (2.4)
. (2.4) , уравнение (1.9) можно записать в виде
, уравнение (1.9) можно записать в виде  . (2.5)
. (2.5) в точке
в точке  .
. в точке
в точке  . (2.6)
. (2.6)