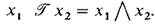Определение и примеры нечёткой логики

Нечёткая логика – логика, основанная на теории нечётких множеств. Её предметом является построение моделей приближенных рассуждений человека и использование их в компьютерных системах. В нечёткой логике расширена граница оценки с двузначной (Либо 0, либо 1) до неограниченной многозначной оценки (На интервале [0,1]).

Нечёткое множество A в полном пространстве X определяется через функцию принадлежности m_A(x):

Логика определения понятия нечёткого множества не содержит какой-либо нечёткости. Вместо указания какого-то конкретного значения (Например 0.8) обычно с помощью нижних и верхних значений задают допустимые пределы оценки (Например [0.7, 0.9]).

В случае нечёткой логики можно создать неограниченное число операций, поэтому в ней не используются базовые операции для записи остальных. Особо важное значение имеют расширения НЕ, И, ИЛИ до нечётких операций. Они называются соответственно – нечёткое отрицание, t-норма и s-норма. Так как число состояний неограниченно, то невозможно описать эти операции с помощью таблицы истинности. Операции поясняются с помощью функций и аксиом, а представляются с помощью графиков.

Аксиоматическое представление нечётких операций:

Нечёткое отрицание

Аксиома N1 сохраняет свойство двузначного НЕ, а N2 – сохраняет правило двойного отрицания. N3 – наиболее существенная: нечёткое отрицание инвертирует последовательность оценок.

Типичная операция нечёткого отрицания – вычитание из 1.

При отрицании значение 0.5 является центральным и обычно x и x^θ принимают симметричные значения относительно 0.5.

T-норма.

Аксиома T1 справедлива, как и для чёткого И. T2 и T3 – законы пересечения и объединения. Аксиома T4 является требованием упорядоченности.

Типичной t-нормой является операция min или логическое произведение:

При логическом произведении график строится симметрично относительно плоскости, образуемый наклонными x1 и x2.

S-норма.

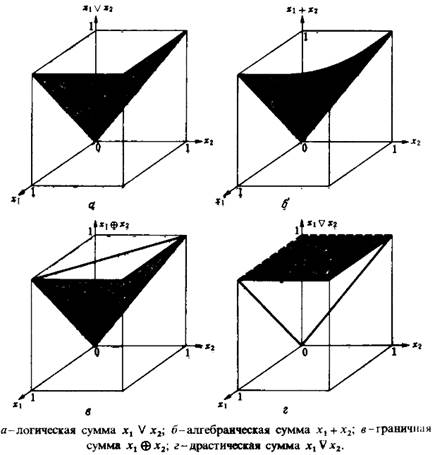
Типичной s-нормой является логическая сумма, определяемая операцией max.

Кроме неё существуют алгебраическая сумма, граничная сумма и драстическая сумма:

Как видно из рисунков порядок обратный, нежели в случае t-нормы.

В качестве примеров нечёткого определения можно рассмотреть температуру и работу клапана:

Сходства

Нечёткая логика является обобщением классической чёткой логики. И чёткая и нечёткая логики основаны на множествах и на операциях отношения. Нечёткие операции являются расширением операций чёткой логики.

Различия

В чёткой логике переменные являются полными членными множеств, а в нечёткой – только частичными членами множеств.

В чёткой логике утверждение либо истинно, либо ложно, в ней действует закон исключения среднего. В нечёткой логике истинность или ложность перестают быть абсолютными и утверждения могут быть частично истинными и частично ложными. В чёткой логике число возможных операций конечно и зависит от количества входов, тогда как в нечёткой логике число возможных операций бесконечно.

3. Пример

Сначала мы рассмотрим множество X всех вещественных чисел между 0 и 10, которые мы назовем областью исследования. Теперь, давайте определим подмножество X всех вещественных чисел в амплитуде между 5 и 8.

A = [5,8]

Теперь представим множество A с помощью символической функции, т.е. эта функция приписывает число 1 или 0 к каждому элементу в X, в зависимости от того, находится ли элемент в подмножестве А или нет. Это приводит к следующей диаграмме:

Мы можем интерпретировать элементы, которым назначено число 1, как элементы которые находятся в множестве А, и элементы, которым назначено число 0, как элементы не в множестве A.

Этой концепции достаточно для многих областей приложений. Но мы можем легко найти ситуации, где теряется гибкость. Чтобы показать это рассмотрим следующий пример, показывающий отличие нечёткого множества от чёткого:

В этом примере мы хотим описать множество молодых людей. Более формально мы можем обозначить

B = {множество молодых людей}

Поскольку, вообще, возраст начинается с 0, нижняя граница этого множества должна быть нулевой. Верхнюю границу, с другой стороны, надо определить. На первый раз определим верхнюю границу множества, скажем, 20 лет. Следовательно, мы получаем B как четкий интервал, а именно:

B = [0,20]

Теперь возникает вопрос: почему кто-то на его 20-ом дне рождения молодой, а на следующий день не молодой? Очевидно, это - структурная проблема, поскольку, если мы перемещаем верхнюю границу от 20 до произвольной точки, мы можем излагать тот же самый вопрос.

Более естественный способ описать множество B состоит в том, чтобы ослабить строгое разделение между молодыми и не молодыми. Мы будем делать это, допуская не только (четкое) решение ДА: он/она находится в множестве молодых, или НЕТ: он/она не в множестве молодых, но более гибких фраз подобно: Хорошо, он/она принадлежит немного больше к множеству молодых или НЕТ, он/она почти не принадлежит к множеству молодых.

В нашем первом примере мы кодировали все элементы Области Исследования 0 или 1. Прямой путь обобщить эту концепцию для нечёткого множества состоит в том, чтобы определить большее количество значений между 0 и 1. Фактически, мы определяем бесконечно многие варианты между 0 и 1, а именно единичный интервал I = [0, 1].

Интерпретация чисел в нечётком множестве, назначенная всем элементам Области Исследования, более трудная. Конечно, снова число 1 назначено элементу как способ определить элемент, который находится в множестве B и 0 - способ, при котором элемент не определен в множестве B. Все другие значения означают постепенную принадлежность к множеству B.

Для большей наглядности, теперь мы показываем множество молодых, подобно нашему первому примеру, графически при помощи символической функции.

При таком способе 25-летние люди будут все еще молоды на 50 процентов (0.5). Теперь Вы знаете, что такое нечеткое множество.

Поиск по сайту: