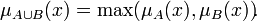 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сходства чётких и нечётких множествСтр 1 из 3Следующая ⇒
Реферат по дисциплине: Прикладные нечёткие системы на тему: СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЧЁТКИХ И НЕЧЁТКИХ МНОЖЕСТВ
Выполнил: студент группы ВТМ-11 Соколов И.П. Проверил: доцент Боцула Л.Н.
2012 г. 1. Сравнительный анализ чёткого и не чёткого множеств Определение и примеры чётких множеств Чёткое множество – совокупность различных элементов, мыслимая как единое целое. X = {x}, x Є X Операции над чёткими множествами: - пересечение: - объединение: - разность (дополнение): - декартово произведение:
Пусть множество цифр E = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, тогда подмножество чётных цифр можно определить как: A = {0, 2, 4, 6, 8}. Пусть множество фамилий E = {Иванов, Петров, Аносов, Кузнецов, Анискин, Афанасьев, Сергеев}, тогда подмножество фамилий, начинающихся на букву “А” можно определить: A = {Аносов, Анискин, Афанасьев}. Определение и примеры нечётких множеств Универсальное множество – множество, содержащие все мыслимые объекты. Нечёткое множество A – математический объект, представляющий собой множество, принадлежность к которому представляет собой не отношение, а функцию; совокупность универсального множества X и характеристической функции μA(x), которая характеризует степень принадлежности элемента x нечёткому множеству.
Функция μA(x) принимает значения в некотором линейно упорядоченном множестве принадлежностей M. Часто в качестве M выбирается отрезок [0, 1]. Если M = {0, 1}, то нечёткое множество может рассматриваться как обычное, чёткое множество.
Отображение элемента в значение 0 означает, что элемент не принадлежит данному множеству, значение 1 соответствует полной принадлежности элемента множеству. Значения, лежащие строго между 0 и 1, характеризуют «нечёткие» элементы. Операции над нечёткими множествами: - пересечение: - объединение: - сумма: - произведение:  Пусть E = {1,2,3,...,100} и соответствует понятию "возраст", тогда нечеткое множество "молодой", может быть определено:m"молодой"(x) =  . Нечеткое множество "молодой" на универсальном множестве E' ={Иванов, Петров, Сидоров,...} задается с помощью функции принадлежности m"молодой"(x) на E = {1,2,3,..100} (возраст),называемой по отношению к E' функцией совместимости, при этом:m"молодой"(Сидоров):= m"молодой"(x), где x - возраст Сидорова.
Сходства чётких и нечётких множеств
Чёткие и нечёткие множества имеют одинаковую иерархию: они делятся на подмножества, множества и надмножества. Чёткие и нечёткие множества имеют одинаковые типы операций (Пересечение, объединение, произведение), производимые над ними. Чёткое множество является частным случаем нечёткого, а понятие нечёткого множества является расширенным понятием, охватывающим и понятие чёткого множества.
Поиск по сайту: |
