 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Технология расширения спектра методом прямой последовательности (DSSS)
Основная идея технологии расширения спектра (Spread Spectrum, SS) заключается в том, чтобы от узкополосного спектра сигнала, возникающего при обычном потенциальном кодировании, перейти к широкополосному спектру. Именно это позволяет значительно повысить помехоустойчивость передаваемых данных. Рассмотрим более детально, как это происходит. При потенциальном кодировании информационные биты 0 и 1 передаются прямоугольными импульсами напряжений. Из курса математики и физики хорошо известно, что любую функцию и соответственно любой сигнал (ограничения, налагаемые на функцию, мы для простоты опускаем) можно представить в виде дискретного или непрерывного набора гармоник — синусоидальных сигналов с определенным образом подобранными весовыми коэффициентами и частотами. Такое представление называют преобразованием Фурье, а сами частоты гармонических сигналов образуют спектральное разложение функции. К примеру, при передаче прямоугольного импульса длительностью T спектр сигнала описывается функцией
Несмотря на бесконечный спектр сигнала, наиболее весомые гармоники, то есть вносящие значительный вклад в результирующий сигнал, сосредоточены в небольшой частотной области, ширина которой обратно пропорциональна длительности импульса. Таким образом, с хорошей степенью точности исходный сигнал можно представить как суперпозицию гармоник в спектральной полосе, ширина которой равна длительности импульса T. Соответственно, чем меньше длительность импульса, тем больший спектральный диапазон занимает такой сигнал. Для того чтобы повысить помехоустойчивость передаваемого сигнала, то есть увеличить вероятность безошибочного распознавания сигнала на приемной стороне в условиях шума, можно воспользоваться методом перехода к широкополосному сигналу, добавляя избыточность в исходный сигнал. Для этого в каждый передаваемый информационный бит «встраивают» определенный код, состоящий из последовательности так называемых чипов
Фактически информационный бит, представляемый прямоугольным имґпульсом, разбивается на последовательность более мелких импульсов-чипов. В результате спектр сигнала значительно уширяется, так как ширину спектра можно с хорошей степенью точности считать обратно пропорциональной длительности одного чипа. Такие кодовые последовательности часто называют шумоподобными кодами. Дело в том, что наряду с уширением спектра сигнала уменьшается и спектральная плотность энергии. То есть энергия сигнала как бы «размазывается» по всему спектру. Результирующий сигнал становится шумоподобным в том смысле, что его теперь трудно отличить от естественного шума. Возникает вопрос — для чего усложнять первоначальный сигнал, если в результате он становится неотличимым от шума? Дело в том, что кодовые последовательности чипов обладают уникальным свойством автокорреляции. Попробуем на интуитивном уровне пояснить, в чем смысл корреляции. Под корреляцией в математике понимают степень взаимоподобия двух функций, то есть насколько две различные функции похожи друг на друга. Соответственно под автокорреляцией понимается степень подобия функции самой себе в различные моменты времени. Например, если некоторая функция зависит (меняется) от времени и эта зависимость выражается в виде Для упрощенного вычисления автокорреляционной функции последовательности Баркера можно рассчитать разницу между числом совпадений и несовпадений между отдельными чипами последовательности при их циклическом почиповом сдвиге относительно друг друга. Как видно из табл. 1, последовательность Баркера обладает ярко выраженным автокорреляционным пиком, соответствующим наложению функции самой на себя. Проведя аналогичные расчеты, нетрудно убедиться, что другие последовательности не обладают подобным свойством, то есть имеют несколько пиков корреляции, которые значительно снижают помехоустойчивость передаваемого сигнала. Таблица 1. Вычисление автокорреляционной функции последовательности Баркера
В приемнике полученный сигнал умножается на код Баркера (вычисляется корреляционная функция сигнала), в результате он становится узкополосным, поэтому его фильтруют в узкой полосе частот, равной удвоенной скорости передачи. Любая помеха, попадающая в полосу исходного широкополосного сигнала, после умножения на код Баркера, наоборот, становится широкополосной, поэтому в узкую информационную полосу попадает лишь часть помехи, по мощности примерно в 11 раз меньшая чем помеха, действующая на входе приемника. Итак, основной смысл использования кодов Баркера заключается в том, чтобы, имея возможность передавать сигнал практически на уровне помех, гарантировать высокую степень достоверности принимаемой информации. Как известно, радиоволны приобретают способность переносить информацию в том случае, если они определенным образом модулируются. При этом необходимо, чтобы модуляция синусоидального несущего сигнала соответствовала требуемой последовательности информационных бит. Существует три основных типа модуляции: амплитудная, частотная и фазовая. В стандарте IEEE 802.11 для передачи сигналов используют фазовую модуляцию, поэтому остановимся на ней более подробно.
Фазовая модуляция Различают два типа фазовой модуляции: собственно фазовую и относительную фазовую модуляцию. При фазовой модуляции (Phase Shift Key, PSK) для передачи логических нулей и единиц используют сигналы одной и той же частоты и амплитуды, но смещенные относительно друг друга по фазе. Например, логический нуль передается синфазным сигналом, а единица — сигналом, сдвинутым по фазе на 180° (рис. 3). Если изменение фазы может принимать всего два значения, то говорят о двоичной фазовой модуляции (Binary Phase Shift Key, BPSK). Математически сигнал, соответствующий логическому нулю, можно представить как Изменение фазы может иметь и более двух значений, например четыре (0, 90, 180 и 270°). В этом случае говорят о так называемой квадратурной фазовой модуляции (Quadrature Phase Shift Key, QPSK) — (рис. 4). Чтобы понять происхождение этого термина, рассмотрим общий вид сигнала, модулированного по фазе: С учетом простейших тригонометрических соотношений данную формулу несложно привести к виду: Из полученного выражения видно, что исходный сигнал можно представить в виде суммы двух гармонических составляющих, смещенных друг относительно друга по фазе на 90°, так как В передатчике, производящем модуляцию, одна из этих составляющих синфазна сигналу генератора, а вторая находится в квадратуре по отношению к этому сигналу (отсюда — квадратурная модуляция). Синфазная составляющая обозначается как I (In Phase), а квадратурная — как Q (Quadrature). Исходный сигнал несложно преобразовать: Если ввести обозначения Кодирующие сигналы di и dq могут принимать значения +1 и –1; учитывая, что При реализации квадратурной фазовой модуляции входной поток бит преобразуется в кодирующую последовательность {dk} так, что логическому нулю соответствует кодирующий бит +1, а логической единице — кодирующий бит –1. После этого кодирующий поток разделяется на четные и нечетные биты. Четные биты поступают в I-канал, а нечетные — в Q-канал. Причем длительность каждого управляющего импульса di и dq в два раза больше длительности исходного импульса dk. Управляющие биты di модулируют по фазе сигнал В приведенной выше схеме квадратурной фазовой модуляции фаза результирующего сигнала может изменяться только каждые 2T секунд. Отличительной особенностью квадратурной фазовой модуляции является наличие четырех дискретных состояний сигнала, отвечающих различным фазам. Это позволяет закодировать в одном дискретном состоянии последовательность двух информационных бит (так называемый дибит). Действительно, последовательность двух бит может иметь всего четыре различные комбинации: 00, 01, 10 и 11. Следовательно, ровно в два раза повышается и скорость передачи данных, то есть бодовая скорость в два раза больше битовой (1 Бод = 2 бит/с). Учитывая, что кодирующему биту +1 отвечает логический нуль, а кодирующему биту –1 — логическая единица, и, принимая во внимание соответствие между фазой сигнала и значениями di и dq, получим таблицу соответствия между входными дибитами и фазами модулированного сигнала (табл. 3). Возможные дискретные состояния сигнала принято изображать на векторной диаграмме состояния или на плоскости сигнального созвездия. При использовании векторной диаграммы состояния каждому значению сигнала ставится в соответствие вектор, длина которого — это условная амплитуда сигнала, а угол поворота вектора относительно горизонтальной оси — это фаза сигнала. То есть векторная диаграмма — это не что иное, как изображение векторов состояния в полярной системе координат. Примеры диаграмм состояния для двоичной и квадратурной фазовой модуляций показаны на рис. 6. Более широкое распространение получил способ отображения различных состояний сигала на сигнальном созвездии. Сигнальное созвездие — это декартова система координат, по оси абсцисс которой откладываются значения кодирующего сигнала di (ось I), а по оси ординат — значения кодирующего сигнала dq (ось Q). В случае двоичной фазовой модуляции плоскость вырождается в прямую, вдоль которой откладываются значения кодирующего сигнала dk. В этом случае на сигнальном созвездии располагаются всего две точки, отвечающие значениям кодирующих битов +1 и –1. Эти две точки соответствуют всем возможным состояниям сигнала. В случае QPSK-модуляции сигнальное созвездие состоит уже из четырех точек с координатами (+1, +1), (+1, –1), (–1, +1), (–1, –1). Эти четыре точки соответствуют четырем возможным дибитам и образуют совокупность всех возможных состояний сигнала (рис. 7). Несмотря на кажущуюся простоту метода фазовой модуляции ему присущи некоторые недостатки, связанные с трудностями технической реализации. Один из недостатков связан с тем, что в случае квадратурной фазовой модуляции при одновременной смене символов в обоих каналах модулятора (с +1, –1 на –1, +1 или с +1, +1 на –1, –1) в сигнале QPSK происходит скачок фазы на 180°. Такие скачки фазы, имеющие место и при обыкновенной двухфазной модуляции, вызывают паразитную амплитудную модуляцию огибающей сигнала. В результате этого при прохождении сигнала через узкополосный фильтр возникают провалы огибающей до нуля. Такие изменения сигнала нежелательны, поскольку приводят к увеличению энергии боковых полос и помех в канале связи. Для того чтобы избежать этого нежелательного явления, прибегают к так называемой квадратурной фазовой модуляции со сдвигом (Offset QPSK, OQPSK). При таком типе модуляции формирование сигнала в квадратурной схеме происходит так же, как и в модуляторе QPSK, за исключением того, что кодирующие биты в Q-канале имеют временную задержку на длительность одного элемента Т. Изменение фазы при таком смещении кодирующих потоков определяется лишь одним элементом последовательности, а не двумя. В результате скачки фазы на 180° отсутствуют, поскольку каждый элемент последовательности, поступающий на вход модулятора синфазного или квадратурного канала, может вызвать изменение фазы на 0, 90 или 270° (–90°). Другим, более серьезным недостатком фазовой модуляции является то обстоятельство, что при декодировании сигнала приемник должен определять абсолютное значение фазы сигнала, так как в фазовой модуляции информация кодируется именно абсолютным значением фазы сигнала. Для этого необходимо, чтобы приемник имел информацию об «эталонном» синфазном сигнале передатчика. Тогда путем сравнения принимаемого сигнала с эталонным можно определять абсолютный сдвиг фазы. Следовательно, необходимо каким-то способом синхронизировать сигнал передатчика с эталонным сигналом приемника (по этой причине фазовая модуляция получила название синхронной). Реализация синхронной передачи достаточно сложна, поэтому более широкое распространение получила разновидность фазовой модуляции, называемая относительной фазовой модуляцией (Differential Phase Shift Keying, DPSK). При относительной фазовой модуляции (также называемой относительной фазовой манипуляцией) кодирование информации происходит за счет сдвига фазы по отношению к предыдущему состоянию сигнала. Фактически приемник должен улавливать не абсолютное значение фазы принимаемого сигнала, а лишь изменение этой фазы. То есть информация кодируется изменением фазы. Естественно, такая модуляция уже не является синхронной и проще реализуется. Во всем остальном DPSK-модуляция не отличается от PSK-модуляции. Для технической реализации DPSK-модуляции входной поток информационных бит первоначально преобразуется, а затем подвергается обычной фазовой модуляции. Если необходимо, чтобы скачки по фазе происходили при появлении логического нуля, то преобразование исходной последовательности сводится к следующему: при появлении нуля происходит преобразование сигнала на инверсный, а при появлении единицы сигнал не меняется. Для примера рассмотрим преобразование 11-чиповой последовательности Баркера по описанному правилу (табл. 4). Данный алгоритм можно записать как логическую операцию неравнозначности над исходной последовательностью и преобразованной последовательностью, задержанной на один бит (смещенной по времени) (рис. 8). Математически это записывается в виде формулы: Аналогично производится преобразование входящей последовательности для получения относительной фазовой модуляции и во втором случае, то есть когда требуется, чтобы фаза сигнала менялась каждый раз при появлении на входе логической единицы. Однако в этом случае формула преобразования будет выглядеть так:
Поиск по сайту: |

 — частота спектральной составляющей
— частота спектральной составляющей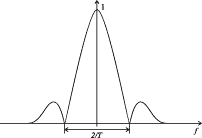

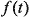 , то можно рассмотреть функцию в некоторый момент времени
, то можно рассмотреть функцию в некоторый момент времени  и в момент времени
и в момент времени  . Степень соответствия этих двух функций друг другу в различные моменты времени и называется автокорреляцией. Оказывается, что можно подобрать такую последовательность чипов, для которой функция автокорреляции, отражающая степень подобия функции самой себе через определенный временной интервал, будет иметь резко выраженный пик лишь для одного момента времени. То есть функция будет подобна самой себе только для одного момента времени и совсем не похожа на себя для всех остальных моментов времени. Одна из наиболее известных (но не единственная) таких последовательностей — код Баркера длиной в 11 чипов: 11100010010. Коды Баркера обладают наилучшими среди известных псевдослучайных последовательностей свойствами шумоподобности, что и обусловило их широкое применение. Для передачи единичного и нулевого символов сообщения используются соответственно прямая и инверсная последовательности.
. Степень соответствия этих двух функций друг другу в различные моменты времени и называется автокорреляцией. Оказывается, что можно подобрать такую последовательность чипов, для которой функция автокорреляции, отражающая степень подобия функции самой себе через определенный временной интервал, будет иметь резко выраженный пик лишь для одного момента времени. То есть функция будет подобна самой себе только для одного момента времени и совсем не похожа на себя для всех остальных моментов времени. Одна из наиболее известных (но не единственная) таких последовательностей — код Баркера длиной в 11 чипов: 11100010010. Коды Баркера обладают наилучшими среди известных псевдослучайных последовательностей свойствами шумоподобности, что и обусловило их широкое применение. Для передачи единичного и нулевого символов сообщения используются соответственно прямая и инверсная последовательности. , а сигнал, соответствующий логической единице, — как
, а сигнал, соответствующий логической единице, — как  . Тогда модулированный сигнал можно записать в виде:
. Тогда модулированный сигнал можно записать в виде:  , где V(t) — управляющий сигнал, принимающий значения +1 и –1. Причем значение сигнала +1 соответствует логическому нулю, а значение сигнала –1 — логической единице.
, где V(t) — управляющий сигнал, принимающий значения +1 и –1. Причем значение сигнала +1 соответствует логическому нулю, а значение сигнала –1 — логической единице. .
. .
.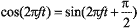

 ;
;  , то получим следующий вид сигнала:
, то получим следующий вид сигнала: 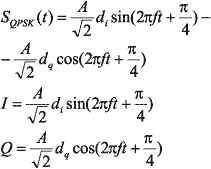
 , получим соотношение между сдвигом фазы и кодирующими сигналами, приведенное в табл. 2.
, получим соотношение между сдвигом фазы и кодирующими сигналами, приведенное в табл. 2.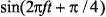 , а биты dq модулируют ортогональный сигнал (смещенный по фазе на 90°), то есть
, а биты dq модулируют ортогональный сигнал (смещенный по фазе на 90°), то есть  . После этого оба сигнала складываются и образуется модулированный сигнал (рис. 5).
. После этого оба сигнала складываются и образуется модулированный сигнал (рис. 5).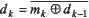 , где mk — исходная последовательность, dk — преобразованная последовательность (при расчетах предполагается, что первый бит преобразованной последовательности равен 1).
, где mk — исходная последовательность, dk — преобразованная последовательность (при расчетах предполагается, что первый бит преобразованной последовательности равен 1). . Пример получения двоичной относительной фазовой модуляции DBPSK показан на рис. 9.
. Пример получения двоичной относительной фазовой модуляции DBPSK показан на рис. 9.