ИЗВРАЩЕНИЯ НА ТЕМУ КУБА 3х3х3

КУБИКИ СОМА

ИСТОРИЯ ПОЯВЛЕНИЯ ГОЛОВОЛОМКИ

Однажды, в 1933 году, известный ученый Вернер Гейзенберг читал публичную лекцию по квантовой физике. Среди слушателей был датский писатель Пит Хейн. Ученый рассказывал о том, как в квантовой механике видоизменяются представления о пространстве, и в ходе пояснения показывал на доске деление пространства на элементарные кубики. У писателя промелькнула мысль об интересной геометрической задаче. Он подумал: а что, если попробовать составить все возможные тела неправильной формы, комбинируя всякий раз не более четырех кубиков одинакового размера? Можно ли из всех этих тел составить куб?

Прервем наш рассказ, чтобы сделать пояснение. Под простейшими телами «неправильной» формы писатель понимал тела, отличающиеся от параллелепипедов. Самое простое из них состоит из трех кубиков. Остальные 6 тел составляются из четырех кубиков. Последние два из них представляют собой зеркальные отображения друг друга.

Вернемся к рассказу о лекции. Пока Гейзенберг рассказывал о квантовой Физике, Хейн рисовал на клочке бумаги комбинации кубиков. В конце концов он убедился, что из семи элементарных тел, действительно можно построить куб. Вернувшись домой, писатель разыскал детские кубики и соорудил из них головоломку уже в натуре. Оказалось, что куб далеко не единственная фигура, которую можно собрать из таких элементов. Хейн увлекся всерьез и придумал больше десятка изящных задач.

Новая игра быстро завоевала популярность. Название головоломки было заимствовано из романа Олдоса Хаксли «О дивный новый мир», в котором сомой назывался наркотик (вероятно, подразумевалось, что головоломка затягивает не хуже наркотика). Каждый, кто хотя бы раз пробовал сложить куб или другую фигуру, надолго «заболевал» головоломкой. И надо сказать, что игра в «кубики для всех» — это не просто развлечение, а замечательная тренировка пространственного воображения. Построение заданных и создание новых фигур развивают пространственное воображение и моторику, снимают стресс.

К этой головоломке имел непосредственное отношение еще один блестящий ученый — британский математик Джон Конвей: в 1961 году он первым определил число ее возможных решений.

В СССР первая публикация на тему кубиков сома появилась в журнале «Наука и жизнь» (№3, 1963 г.). Позже журнал неоднократно возвращался к этой головоломке.

Начинать, разумеется, надо с решения легких задач. Первое, сравнительно нехитрое задание — сборка куба 3х3х3. Существует 240 способов это сделать (если не считать повороты и зеркальные отражения). Вот один из способов сложения куба:

Освоив куб, приступайте к сооружению более сложных фигур.

* * *

МЕТОД ПОИСКА ВСЕХ ВОЗМОЖНЫХ ВАРИАНТОВ ПОСТРОЕНИЯ КУБА

(Автор – Дмитрий Филатов)

Рассмотрим варианты построения куба, когда элементы 5 и 6 или 5 и 7 образуют фигуру, показанную на фото 1. В этом случае нижний слой выглядит следующим образом:

Заполнение третьей строчки нижнего слоя начнём с элемента 7. В дальнейшем будем делать по-другому, начинать будем с элемента 1 и так далее перебирать элементы в порядке увеличения их номера. Начинать будем слева и двигаться направо. Начинать будем с такого положения элемента, когда он занимает наибольшее количество мест слоя. При вращении элемента будем это делать с левой стороны и рассматривая варианты поворачивает его по часовой стрелке. данная технология поиска вариантов позволяет найти все возможные варианты, не пропустив ни одного. Положение

как ни странно не даёт ни одного варианта. А вот это положение, показанное на фото 2:

даёт целых 5 вариантов:

Если фигура 7 в третьей строке нижнего слоя занимает только 1 позицию, то это даёт только 3 варианта:

Теперь варианты, когда третью строку занимает один или два кубика элемента 3. Если в третьей строке два кубика, то возможен только один вариант:

Если в третьей строке один кубик элемента 3, то возможен представленный ниже вариант:

Думаю, метод поиска решений теперь понятен. Дальше предлагаю поискать самим.

* * *

ИЗВРАЩЕНИЯ НА ТЕМУ КУБА 3х3х3

ШАХМАТНЫЙ КУБ

Куб придумал Виктор Дымский.

Из семи элементов «Кубиков СОМА», раскрашенных соответствующим образом, соберите куб так, чтобы на всех его гранях темные и светлые квадратики чередовались в шахматном порядке.

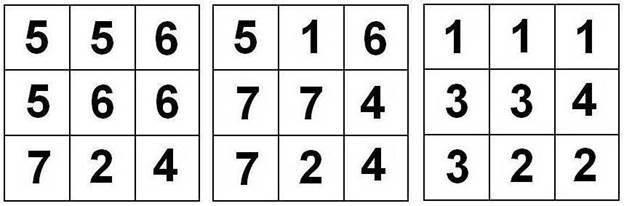
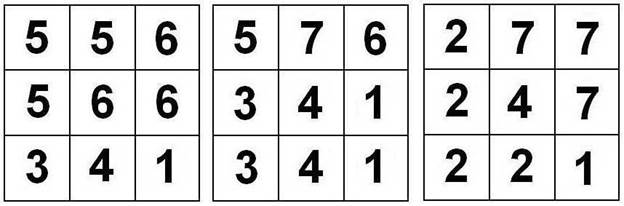
Каждый кубик, входящий в элемент, имеет по три темных и три светлых грани, причем противоположные грани имеют различную расцветку. Ориентация кубиков в элементах показана на рис. 1 и 2. Рис. 2 дополняет рис. 1, и на нем элементы расположены так, что видны те грани кубиков, которые не видны на рис. 1.

Задача имеет единственное решение, и возможность того, что куб случайно будет правильно сложен, практически исключена. Прежде чем его сложить, придется почувствовать весьма тонкие особенности элементов, из которых составляется куб.

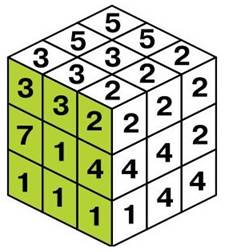
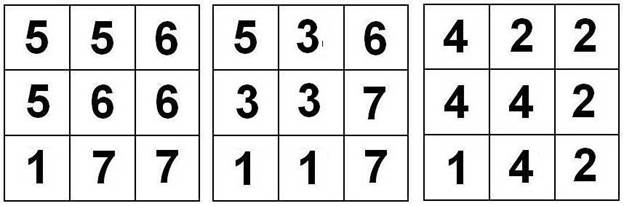
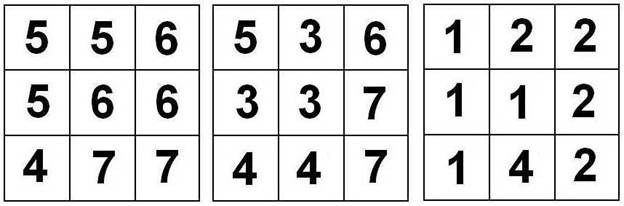
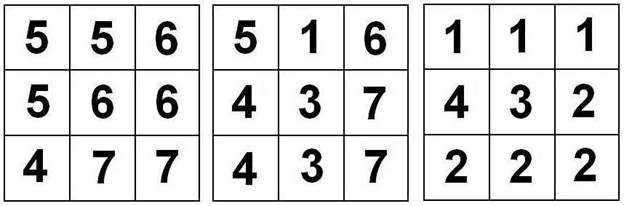
ИГРАЛЬНАЯ КОСТЬ

Куб придумала Ирина Новичкова.

Из семи элементов «Кубиков СОМА», раскрашенных соответствующим образом, соберите куб так, чтобы на его гранях, как на игральном кубике, было от 1 до 6 очков.

Вот маркировка элементов головоломки:

Автор утверждает, что решение единственное.

Поиск по сайту: