|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лістинг 4.3 Графік функції (використання методу Polyline)
procedureTForml.Button1Click(Sender: TObject); Var gr: array[1..50] ofTPoint; // графік — ламана лінія x0,y0: integer; // координати точки початку координат dx,dy: integer; // крок координатної сітки по осях X і Y i: integer; begin х0 := 10; у0 := 200; dx :=5;dy := 5; // заповнимо масив gr fori:=l to50 do begin gr[i].x := x0 + (i-l)*dx; gr[i].y := y0 - Data[i]*dy; end; // будуємо графік withforml.Canvas do begin MoveTo(x0,y0); LineTo(x0,10); // вісь Y MoveTo(x0,y0); LineTo(200,y0); // вісь X Polyline(gr); // графік end; end;
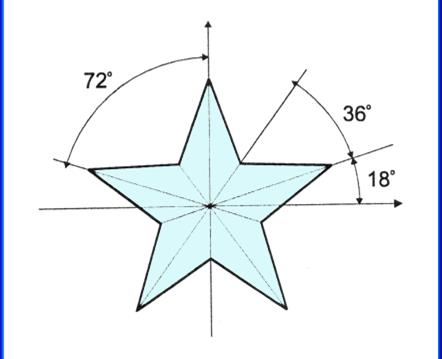
Метод Polyline можна використовувати для креслення замкнутих контурів. Для цього треба, щоб перший і останній елементи масиву містили координати однієї і тієї ж крапки. Як приклад використання методу Polyline для креслення замкнутого контуру в лістингу 4.4 приведена програма, що на поверхні діалогового вікна, у точці натискання кнопки миші, вичерчує контур п'ятикутної зірки (мал. 4.5). Колір, яким викреслюється зірка, залежить від того, яка з кнопок миші була натиснута. Процедура обробки натискання кнопки миші (подія MouseDown) викликає процедуру малювання зірки starLine і передає їй як параметр координати точки, у якій була натиснута кнопка. Зірку вичерчує процедура starLine, що як параметри одержує координати центра зірки і полотно, на якому зірка повинна бути виведена. Спочатку обчислюються координати кінців і западин зірки, що записуються в масив р. Потім цей масив передається як параметр методу Polyline. При обчисленні координат променів і западин зірки використовуються функції sin і cos. Тому що аргумент цих функцій повинний бути виражений у радіанах, то значення кута в градусах домножується на величину pi/180, де pi — це стандартна іменована константа рівна числу π.
Лістинг 4.4 Креслення замкнутого контуру (зірки) у точці натискання кнопки миші
unitStars_; Interface Uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls; Type TForm1 = class(TForm) procedureFormMouseDown(Sender: TObject; Button: TMouseButton; Shift: TShiftState; X, Y: Integer); Private { Private declarations } Public { Public declarations } end; Var Forml: TForml; Implementation {$R *.dfm} // вичерчує зірку procedureStarLine(x0,y0,r: integer; Canvas: TCanvas); // x0,y0 — координати центра зірки //r — радіус заїзди var р : array [1.. 11] ofTPoint; // масив координат променів і западин a: integer; // кут між віссю ОХ і прямої, що з'єднує // центр зірки і кінець чи лучачи западину i: integer; Begin а := 18; // будуємо від правого гор. променя fori:=l to10 do begin if(i mod2=0) then begin// западина p[i].x := x0+Round(r/2*cos(a*pi/180) ) ; p[i] .y:=y0-Round(r/2*sin(a*pi/180) ) ; End Else begin //промінь [i] .x:=x0+Round(r*cos (a*pi/180) ) ; [i] .y:=y0-Round(r*sin(a*pi/180) ) ; end; a := a+46; end; p[ll].X := p[l].X; // щоб замкнути контур зірки Canvas. Polyline (р) ; // накреслити зірку end; // натискання кнопки миші procedureTForm1 . FormMouseDown { Sender : TObject; Button: TMouseButton; Shift: TShiftState; X, Y: Integer); Begin ifButton = mbLeft // натиснута ліва кнопка? thenForm1. Canvas . Pen . Color : = clRed elseForm1. Canvas. Pen. Color := clGreen; StarLine(x, y, 30, Forml. Canvas ); end; End.
Рис.4.5Зірка Примітка Зверніть увагу, що розмір масиву р на одиницю більше, ніж кількість кінців і западин зірки, і що значення першого й останнього елементів масиву збігаються.
Окружність і еліпс
Метод Ellipse вичерчує чи еліпс окружність, у залежності від значень параметрів. Інструкція виклику методу в загальному виді виглядає в такий спосіб:
Поиск по сайту: |