 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Проверочный расчет передачи
Условие контактной прочности передачи имеет вид Контактные напряжения равны
где Zσ- коэффициент вида передачи, Zσ = 8400 для косозубой передачи, KН - коэффициент контактной нагрузки, KН = KHα KHβ KНV. Коэффициент неравномерности распределения нагрузки между зубьями KHα =1+ A (nст – 5) Kw =1+0.15(8-5)·0.293=1.13 где А = 0.06 для прямозубых и А = 0.15 для косозубых и шевронных передач; Kw - коэффициент, учитывающий приработку зубьев. При НВ2 < 350 Kw = 0.002НВ2 + 0.036(V – 9)=0.002·248.5+0.036(1.94-9)=0.293 Коэффициент неравномерности распределения нагрузки по ширине колеса KHβ =1+ (K где K
K Динамический коэффициент определим по табл. 10.1 [1] KНV=1.02 Окончательно получим KH=1.13·1.015·1.02=1.17 Расчетные контактные напряжения
σH =
Допускается перегрузка по контактным напряжениям не более 5%, рекомендуемая недогрузка до 15%.Так как σH>σHP, выполним расчет перегрузки по контактным напряжениям:
Условия изгибной прочности передачи имеют вид sFj Напряжение изгиба в зубьях шестерни
где YF1 - коэффициент формы зуба; KF - коэффициент нагрузки при изгибе;
Yb - коэффициент, учитывающий влияние угла наклона зуба на его прочность (для косозубой передачи Yb= 0.52): Yb= 1 - Yε - коэффициент, учитывающий перекрытие зубьев: Yε = Здесь εα – коэффициент торцевого перекрытия, который для нулевых передач приближенно определяют по формуле εα = [1.88 – 3.2( Напряжение изгиба в зубьях колеса
Коэффициенты формы зуба YFj=3.47 + где ZVj - эквивалентное число зубьев, для прямозубых передач ZVj = Zj, для непрямозубых передач ZVj = ZV1 = 42.7 ZV2 =192.3
YF1 = 3.47 +
Коэффициент нагрузки при изгибе KF = KFα KFβ KFV =1.45·1.041·1.03=1.55 Коэффициент неравномерности распределения нагрузки между зубьями KFα =1+0.15(8-5)=1.45 Коэффициент неравномерности распределения нагрузки по ширине колеса KFβ = 0.18 + 0.82K Динамический коэффициент при НВ2 < 350 KFV = 1+ 1.5(KHV – 1)=1+1.5(1.02-1)=1.03 Напряжения изгиба sF1= 3.78·0.52·
sF2=
Допускается перегрузка по напряжениям изгиба не более 5 %, недогрузка не регламентируется. Условия изгибной прочности передачи выполняются, поскольку sF1
Силы в зацеплении Окружная сила Ft = Распорная сила Fr = Ft Осевая сила
3. Расчет клиноременной передачи
Исходные данные Крутящий момент на ведущем шкиве Т1 =173.7 Н•м Частота вращения ведущего шкива n1=973 мин-1 Передаточное число u= 2.25 Относительное скольжение Тип нагрузки - Переменная Число смен работы передачи в течение суток nc= 2
Расчет передачи
1. Выбор ремня По величине крутящего момента на ведущем шкиве выбираем ремень со следующими параметрами (табл. 1.3) [1]: тип сечения - B; площадь поперечного сечения A= 230 мм2; ширина нейтрального слоя bp= 19 мм; масса погонного метра ремня qm= 0.3 кг/м.
2. Диаметры шкивов Диаметр ведущего шкива определим по формуле (1.3) [1]: d1 = 40 Округлим d1 до ближайшего значения из ряда на с. 77 [1]: d1= 224 мм. Диаметр ведомого шкива равен: d2 = u После округления получим: d2=500 мм. 3. Фактическое передаточное число uф = 4. Предварительное значение межосевого расстояния
5. Длина ремня L = 2 L = 2·579.2+0.5 Округлим до ближайшего числа из ряда на с.77 [1]: L = 2500 мм. После выбора L уточняем межосевое расстояние
a=0.25(2500-1137.26+ где W = 0.5 Y = 2 (d2 – d1)2=2(500-224)2=152352 мм2 6. Угол обхвата на ведущем шкиве
7. Скорость ремня V = 8. Окружное усилие равно Ft = 9. Частота пробегов ремня
10. Коэффициент, учитывающий влияние передаточного числа на напряжения изгиба в ремне, Cu=1.14 – 11. Приведенное полезное напряжение для ремней нормального сечения
12. Допускаемое полезное напряжение [ где C C Cp – коэффициент режима работы. Cp = Cн – 0.1(nc – 1)=0.85-0.1(2-1)=0.75 Cн – коэффициент нагружения, Cн =0.85 13. Расчетное число ремней Z = где Сz - коэффициент, учитывающий неравномерность распределения нагрузки между ремнями (табл. 3.3) [1], предварительно приняли Сz=0.95. Расчетное значение Z округлим до ближайшего большего целого числа Z=5 14. Сила предварительного натяжения одного ремня S0 = 0.75 15. Сила, нагружающая валы передачи, Fb = 2 S0 Z sin
Расчет валов
Поиск по сайту: |

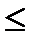
 .
.  =
= 
 ,
, – 1) Kw,
– 1) Kw, = 0.5
= 0.5  (u + 1)=0.5·0.4(4.5+1)=1.1
(u + 1)=0.5·0.4(4.5+1)=1.1
 =501.3 МПа
=501.3 МПа σH =100
σH =100  =100
=100
 ,
,

 +
+  )] cos β
)] cos β .
. + 0.092
+ 0.092  ,
, .
. =3.78 YF2 =3.47 +
=3.78 YF2 =3.47 +  =3.54
=3.54 =0.18+0.82·1.05=1.041
=0.18+0.82·1.05=1.041 =147.1 МПа < σFP1
=147.1 МПа < σFP1 =145.4 МПа < σFP2
=145.4 МПа < σFP2 =
= 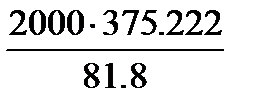 =9174 Н
=9174 Н = 4486
= 4486  = 3414 Н
= 3414 Н Н
Н = 0.015
= 0.015 = 223.1 мм.
= 223.1 мм. d1 = 1.48(1-0.015)224= 496.4 мм.
d1 = 1.48(1-0.015)224= 496.4 мм.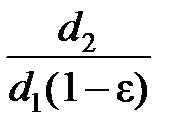 =
= 
 = 0.8 (d1 + d2)= 0.8(224+500)=579.2 мм.
= 0.8 (d1 + d2)= 0.8(224+500)=579.2 мм. + 0.5
+ 0.5  (d1 + d2) +
(d1 + d2) + 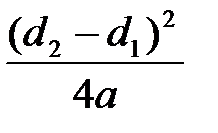
 = 0.25(L – W +
= 0.25(L – W +  )
) ) = 667.1 мм.
) = 667.1 мм. (d1 + d2)=0.5
(d1 + d2)=0.5  =
=  – 57.
– 57. 
 = 156.29º
= 156.29º =
=  = 11.41 м/с
= 11.41 м/с =
=  = 1551 Н
= 1551 Н =
=  =
=  = 4.56 (1/с)
= 4.56 (1/с) = 1.14-
= 1.14-  =1.13
=1.13 =
=  –
–  – 0.001V2 =
– 0.001V2 =  -
-  = 2.3 МПа
= 2.3 МПа ] =
] =  C
C  Cp= 2.3·0.94·0.75=1.62 МПа
Cp= 2.3·0.94·0.75=1.62 МПа – коэффициент, учитывающий влияние угла обхвата,
– коэффициент, учитывающий влияние угла обхвата, = 1-0.44 ln
= 1-0.44 ln 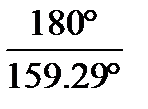 =0.94
=0.94 =
=  = 4.38
= 4.38 + qmV2= 0.75
+ qmV2= 0.75  +0.3·11.412= 0.37 кН
+0.3·11.412= 0.37 кН = 2·369·5· sin
= 2·369·5· sin  = 3.63
= 3.63