 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Термодинамическое описание молекулярного раствораСтр 1 из 4Следующая ⇒
Растворы и реакции в растворах 4.1. Состав раствораиз I компонентов характеризуется следующими концентрационными единицами (1 ≤ i ≤ I, Mi – мольные массы компонентов,ρ, ρ1, г/см3 – плотности раствора и чистого растворителя): 1) ni –число молей i-го компонента. 2) xi = ni /n – мольная или молярнаядоля, где 3) Моляльность m2 – число молей растворенного вещества (компонента 2) в 1 кг растворителя с индексом 1
4) Объемная концентрация ci = ni /V,моль/м3 (CИ). Молярная концентрация или молярность С2, (моль/л ≡ М)наиболее распространена в химической практике. Взаимосвязь молярности и моляльности для бинарного раствора осуществляется формулой: 5) Кроме молярности в химии используется еще одна разновидность объемной концентрации – нормальность, взаимосвязанная с понятием эквивалента и равная числу моль-эквивалентов в 1 литре раствора.
Химический эквивалент –это условная частица в целое число раз (z*) меньшая или равная соответствующей формульной единице вещества.Эк = 1/z*, где z* - эквивалентное число. (Ранее z*(Fe2(SO4)3) = 2*v = 6, Эк =1/6.) Таким образом, веществу в количестве n молей соответствует nэ = z*n его моль-эквивалентов, а потому Сэ, н.= z* С, М. Примеры, определяющие эквивалент вещества в химической реакции: Al2(SO4)3+12KOH=2K3[Al(OH)6]+3K2SO4, Эк(Al2(SO4)3)=n1/n2=1/12, z*=12. H2 SO4 + 2 KOH = K2 SO4 + 2H2O, Эк(H2 SO4) =1/2, z*= 2 H2 SO4 + KOH = KHSO4 + H2O, Эк(H2 SO4) = 1, z*=1, (исходно z*– число атомов Н, замещаемых металлом или замещающих металл в реакции). Напомним, мольная масса эквивалента Мэ = M ·Эк = M/z*. Термодинамическое описание молекулярного раствора В химическом потенциале i-го компонента (3.41') в идеальном конденсированном (твердом или жидком) растворе: Энергия Гиббса бинарного раствора из n1и n2 молей веществ:
К идеальной её части согласно (3.40) добавлены энергетические и структурные составляющие энергии Гиббса реального раствора. При этом использовано Ван–Лааровское приближение регулярного раствора (А – параметр взаимодействия). Химические потенциалы по определению (3.41'') соответствуют частным производным от энергии Гиббса по числу молей. Опуская технические детали дифференцирования, приведем конечный результат
Активности растворенных веществ ввел Льюис. Это позволило в выражениях для реальных растворов сохранить форму идеальных. При этом активность компонента трактуется какисправленная концентрация. Равновесие гетерогенной реакции испарения, исходя из условия (3.45), характеризуется равенством хим. потенциалов компонентов в жидкости (4.2) и паре (3.41) и определяет давление насыщенных паров:
Введенное обозначение При А = 0 из (4.3) получается Pi =P0i xi - закон Рауля для идеального раствора. При А > 0 энтальпия – положительна, смешение компонентов энергетически не выгодно, и растворенное вещество становится более летучим.
При достаточно больших отношениях А/(RT) на кривой Р1(Т) появляется ниспадающий участок (пунктир), который соответствует термодинамически неустойчивым состояниям. Температурная зависимость максимумов х1' и минимумов х1'' серии таких кривых представлена на рис. 4.2. Заштрихованная часть ниже критической температуры Тсраствора соответствует области, где система расслаивается на два несмешивающихся раствора, один из которых образован преимущественно вторым компонентом (х1'), а другой – первым (х1'').
Общее давление над раствором Р = Р1 + Р2 как сумма парциальных (4.3) и состав пара y2 = P2/P в зависимости от состава жидкости x2. представлены на рис. 4.3 в виде т.н. диаграммы равновесия жидкость-пар.
Диаграммы фазовых равновесий жидкость - пар и твердое тело – жидкость − основа обширной области прикладной химии – технологии разделения и очистки веществ. В молекулярных растворах деление на растворитель и растворенное вещество носит условный характер и часто определяется преобладающей концентрацией одного из компонентов. Такое описание используют в нефтеперегонке, технологии высокочистых веществ, при разделении изотопов и др. Кстати….. (история о получении изотопа чистого урана для атомной промышленности, низкотемпературная ректификация, ультрацентрифугирование, Машзавод, ОКБМ…)
Растворы электролитов Значительное число гетерополярных химических соединений под действием полярных растворителей, среди которых наиболее характерным является вода, испытывают кардинальную структурно-энергетическую перестройку при растворении. Поляризующее взаимодействие растворителя приводит к диссоциации растворенного вещества на сольватированные заряженные фрагменты, которые называют ионами. В физике такие образования называют квазичастицами с эффективными массами и размерами, иногда значительно отличающимися от исходных «голых» частиц. Их принципиальная роль в описании конденсированных фаз заключается в том, что они включают в себя значительную часть энергетики их образования. Это упрощает описание, сводя систему преобразованных частиц-ионов к почти идеальной системе, с достаточно слабым межионным взаимодействием. При таком подходе выделяется роль растворителя, который, сыграв активную роль в образовании ионов, превращается в фоновую среду. Сильные электролиты −
Пример: CaCl2 → Ca2+ + 2Cl ¯ (z+ = 2, z− = -1 ). Если m – моляльность растворенного вещества (электролита), то моляльности положительных и отрицательных ионов: m+ = ν+m , m− = ν− m. Применим льюисовское определение химического потенциала компонента к неидеальной системе ν = ν++ ν− взаимодействующих ионов
где коэффициенты активности γ+ и γ− соответствуют моляльностям. Ввиду невозможности их отдельного определения используется среднеионный коэффициент активности: а химический потенциал электролита приобретает вид:
Физически обоснованный результат статистической теории Дебая-Хюккеля для разбавленных растворов (без вывода) известен под названием предельного закона. где
- коэффициент Aγ(Т)кроме физических постоянных (числа Авогадро и постоянной Больцмана) включает в себя: ε – относительную диэлектрическую проницаемость (78,54 (H2O)); ρ – плотность раствора, г/см3 (для разбавленного раствора при 25о С ρH2O = 0,997 г/см3). Значения Aγ для ряда растворителей при 25oC равны:0,51 (H2O); 1,778 (СH3OH); 3,7613 (ацетон). Несмотря на ограниченную концентрационную область применимости (≤ 0,01М) теория Дебая-Хюккеля имеет большое теоретическое значение, поскольку эмпирически установленная зависимость lg γ±от I1/2 получила обоснование с позиции статистической физики. Выводы: 1. γ± → 1 при m → 0, т.е. при значительном разбавлении γ± можно считать равным 1, а раствор становится идеальным. 2. Стандартные энтальпии и энтропии образования ионов содержатся в
Поиск по сайту: |

 . Формула обратного пересчета моляльности в мольную долю
. Формула обратного пересчета моляльности в мольную долю 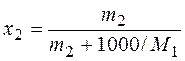 получается из 2).
получается из 2).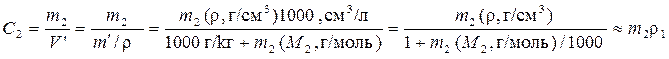 ,где V' и m' – объем и масса растворителя с растворенным веществом на 1 кг растворителя. Последнее равенство справедливо при малых m2 , т.е. для разбавленных растворов. Для разбавленного водного раствора молярность С2 и моляльность m2 численно близкие величины (ρ1 ≈ 1 г/см3).
,где V' и m' – объем и масса растворителя с растворенным веществом на 1 кг растворителя. Последнее равенство справедливо при малых m2 , т.е. для разбавленных растворов. Для разбавленного водного раствора молярность С2 и моляльность m2 численно близкие величины (ρ1 ≈ 1 г/см3). , (моль-экв/л º н.)
, (моль-экв/л º н.) упростим обозначение
упростим обозначение  , мольной (черта сверху) энергии Гиббса чистого i-го вещества.
, мольной (черта сверху) энергии Гиббса чистого i-го вещества.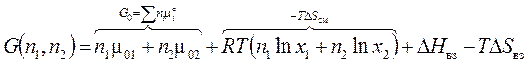 (4.1)
(4.1) ,
,  . (4.1')
. (4.1') , который можно представить в виде:
, который можно представить в виде: (4.2), где
(4.2), где  - активность, (4.2')
- активность, (4.2') - коэффициент активности. (4.2'')
- коэффициент активности. (4.2'')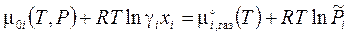 .
.  ,
, (4.3)
(4.3) , как следует из (4.3) при xi → 1, соответствует давлению насыщенного пара чистого i-го компонента.
, как следует из (4.3) при xi → 1, соответствует давлению насыщенного пара чистого i-го компонента. Рис. 4.1. Зависимости парциального давления пара 1-го компонента от состава бинарного раствора при различных значениях параметра А.
Рис. 4.1. Зависимости парциального давления пара 1-го компонента от состава бинарного раствора при различных значениях параметра А.
 Рис. 4.2. Области существования и расслаивания (заштрихована) двухфазной системы. Тс - критическая температура.
Рис. 4.2. Области существования и расслаивания (заштрихована) двухфазной системы. Тс - критическая температура.

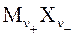 при растворении практически полностью диссоциируют на ν+ число положительных (
при растворении практически полностью диссоциируют на ν+ число положительных (  ) и ν− число отрицательных (
) и ν− число отрицательных (  ) ионов согласно уравнению реакции диссоциации (ионизации):
) ионов согласно уравнению реакции диссоциации (ионизации): (заряды ионов z+ > 0, z− < 0) . (4.4)
(заряды ионов z+ > 0, z− < 0) . (4.4)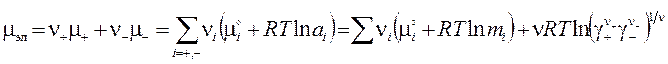 ,
,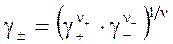 , (4.5)
, (4.5) , (4.6)
, (4.6) , (4.7)
, (4.7) - ионная сила;
- ионная сила;
 и составляют важнейшую справочную информацию.
и составляют важнейшую справочную информацию.