 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Оптические свойства дисперсных систем
При прохождении света через дисперсную систему в зависимости от природы и размера частиц дисперсной фазы можно наблюдать: а) поглощение излучения, б) его отражение, в) его рассеяние (опалесценция). В случае истинных растворов, где растворенное вещество присутствует исключительно в виде молекул или ионов, можно наблюдать лишь поглощение света, связанное с изменением электронного состояния растворенных частиц, и если они поглощают излучение из видимой области спектра, то раствор будет окрашен. Для коллоидных систем эффект поглощения имеет место, если дисперсная фаза состоит из окрашенных частиц. Если же коллоидный раствор не поглощает в видимой области спектра, то его называют белым золем, а проявление эффектов отражения и рассеяния зависит от соотношения между длиной волны падающего излучения λ и размерами частиц дисперсной фазы r, где r – эффективный радиус частицы: · если размер частиц 2r >> λ, то имеет место отражение; · если размер частиц 2r << λ, то имеет место рассеяние.
Интенсивность рассеянного света зависит от длины падающего излучения, размера, формы и концентрации рассеивающих частиц, оптических свойств дисперсионной среды и дисперсной фазы. В 1871 г. Релеем была предложена теория упругого рассеяния света, которая установила взаимосвязь между указанными переменными. Используя эту взаимосвязь, можно достаточно просто оценить размеры коллоидных частиц в опытах по рассеиванию света белыми золями, где мерой светорассеяния является мутность дисперсной системы τ, которую в свою очередь рассчитывают по величине измеряемой в опыте оптической плотности А коллоидного раствора (турбодиметрия). Величина мутности τ задает долю интенсивности общего светового потока, рассеянного по всем направлениям единицей объема (1 см3) белого золя Iрасс, относительно интенсивности падающего монохроматического излучения I0 с данной длиной волны: Для белых золей рассеянный свет рассматривается как фиктивно поглощенный, поскольку потеря интенсивности падающего излучения при прохождении его через коллоидный раствор связана не с эффектом поглощения (он по определению отсутствует у белых золей), а с тем, что часть вторичного излучения за счет изменения направления распространения световой волны проходит мимо фотоэлемента спектрометра, регистрирующего интенсивность прошедшего излучения Iпрош. Это позволяет связать мутность белого золя с измеряемой в опыте его оптической плотностью:
где τ – мутность белого золя,см–1;
l – толщина рассеивающего слоя коллоидного раствора (длина кюветы), см.
где n1 и nо – показатели преломления дисперсной фазы и дисперсионной среды соответственно; n – концентрация частиц дисперсной фазы, частиц/см3; V – объем коллоидной частицы, см3; l = lвакуум/nо – длина световой волны в данной дисперсионной среде, см. Теория рассеяния света дисперсными системами, разработанная Рэлеем, показывает, что интенсивность рассеянного света обратно пропорциональна длине волны падающего света в четвертой степени, т.е. коротковолновое излучение рассеивается более интенсивно, чем длинноволновое. Красный свет имеет наибольшую в видимой области спектра длину волны (620-760 нм) и рассеивается в меньшей степени, поэтому запрещающие сигналы светофоров и других регулирующих устройств имеют красный цвет – он виден на больших расстояниях. Наоборот, сине-фиолетовый свет (380-450 нм) интенсивно рассеивается аэрозольными частицами воздуха и может быть использован для светомаскировки. Голубой цвет чистого неба обеспечивают рассеянные на неоднородностях атмосферы сине-фиолетовые лучи от находящегося в зените Солнца, а красновато-оранжевую окраску неба во время закатов и рассветов – прошедшие сквозь толщу атмосферы прямые лучи от Солнца, находящегося на линии горизонта. На практике некоторые требования теории Релея могут нарушаться, что не позволяет корректно использовать уравнение (3). Например, с увеличением размера частиц и при условии использования излучения из видимой области спектра нарушается критерий r £ 0,05l и закономерность τ ~ l-4 перестает быть справедливой. В этом случае для оценки размеров частиц используют полуэмпирическую форму уравнения Релея, в которой показатель степени «4» у длины волны заменен на эмпирический параметр «n»:
Экспериментальное определение параметра n для данного белого золя связано с установлением зависимости его мутности τ от длины волны падающего (рассеянного) излучения (спектр мутности). С этой целью измеряют оптическую плотность A коллоидного раствора при нескольких длинах волн в интервале 400-700 нм, затем по формуле (2) рассчитывают мутность τ и строят спектр мутности (рисунок 2).
Само же значение показателя n находят графически на основе логарифмической формы уравнения (4), где все характеристики белого золя объединены в виде const – при определении спектра мутности они на меняются:
Это уравнение прямой линии в координатах
Значение показателя степени n зависит от соотношения между радиусом коллоидной частицы и длиной волны рассеянного излучения, которое представляют в виде безразмерного параметра z:
причем по мере сближения значений r и λ показатель степени n меняется от 4 до 2. Опытным путем была определена градуировочная зависимость между показателем степени n и параметром z, приведенная в таблице 1. Таблица 1 – Связь между параметром z и показателем степени n
Таким образом, оценка размеров коллоидных частиц белых золей сводится к экспериментальному определению показателя степени n, по величине которого определяют значение параметра z с использованием градуировочного графика z = f(n). Далее по формуле (6) рассчитывают среднее значение радиуса частиц r, где длину волны λ для данной дисперсионной среды берут как среднее между минимальной и максимальной длиной волны в интервале, где снят спектр мутности (показатель преломления воды n0 = 1,333):
Поиск по сайту: |
 Рассеяние – это превращение части падающего света во вторичное излучение за счет упругого взаимодействия падающего излучения с коллоидной частицей, при этом во вторичном излучении сохраняется исходное значение длины волны λ, но изменяется направление распространения световой волны. Рассеяние приводит к тому, что луч света в дисперсных системах становится видимым и это проявляется в так называемом эффекте Тиндаля (рисунок 1). Если на коллоидный раствор направить луч света, например, лазерной указки, то сбоку можно наблюдать освещенный конус (конус Тиндаля).
Рассеяние – это превращение части падающего света во вторичное излучение за счет упругого взаимодействия падающего излучения с коллоидной частицей, при этом во вторичном излучении сохраняется исходное значение длины волны λ, но изменяется направление распространения световой волны. Рассеяние приводит к тому, что луч света в дисперсных системах становится видимым и это проявляется в так называемом эффекте Тиндаля (рисунок 1). Если на коллоидный раствор направить луч света, например, лазерной указки, то сбоку можно наблюдать освещенный конус (конус Тиндаля). . (1)
. (1) ,
,
 – его оптическая плотность, измеряемая на спектрометре относительно дистиллированной воды, I0, Iпрош – интенсивности падающего и прошедшего монохроматического излучения, причем I0 = Iпрош + Iрасс.;
– его оптическая плотность, измеряемая на спектрометре относительно дистиллированной воды, I0, Iпрош – интенсивности падающего и прошедшего монохроматического излучения, причем I0 = Iпрош + Iрасс.; было рассчитано Релеем для разбавленного белого золя со
сферическими частицами, радиус которых должен быть гораздо меньше длины волны:
r
было рассчитано Релеем для разбавленного белого золя со
сферическими частицами, радиус которых должен быть гораздо меньше длины волны:
r  0,05l, т.е. если в опыте использовать монохроматическое излучение из видимой области спектра с длинами волн от 400 до 780 нм, то радиус определяемых частиц не должен превышать
40 ¸ 50 нм:
τ =
0,05l, т.е. если в опыте использовать монохроматическое излучение из видимой области спектра с длинами волн от 400 до 780 нм, то радиус определяемых частиц не должен превышать
40 ¸ 50 нм:
τ =  3(
3(  )2
)2  , (3)
, (3)
 .
.
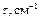

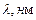 Рисунок 2 – Спектр мутности
белого золя
Рисунок 2 – Спектр мутности
белого золя
 = const’
= const’  .
.
 от
от  (рисунок 3), а ее угловой коэффициент равен (–n).
(рисунок 3), а ее угловой коэффициент равен (–n).
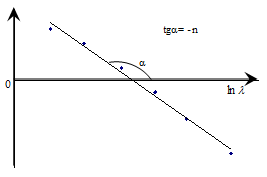 Рисунок 3 – К расчету эмпирического параметра n в уравнении Релея
Рисунок 3 – К расчету эмпирического параметра n в уравнении Релея
 ,
,
 .
.