 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие функционального ряда и степенного ряда ⇐ ПредыдущаяСтр 4 из 4
Функциональный же ряд состоит из ФУНКЦИЙ:
В общий член ряда Наиболее популярной разновидностью функционального ряда является степенной ряд. Определение: Степенной ряд – это ряд, в общий член Лишь бы показатели степеней при «иксАх» были натуральными.
Сходимость степенного ряда. Прошу любить и жаловать степенной ряд Переменная Очевидно, что, подставляя в Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая: 1) Степенной ряд сходится абсолютно на некотором интервале Радиус сходимости, если совсем просто, это половина длины интервала сходимости: Геометрически ситуация выглядит так:
В данном случае, интервал сходимости ряда: Широко распространен тривиальный случай, когда интервал сходимости симметричен относительно нуля:
Здесь интервал сходимости ряда: А что будет происходить на концах интервала – Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: – Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости рядапредставляет собой полуинтервал: – Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: Термины очень похожи, область сходимости ряда – это чуть более детализированныйинтервал сходимости ряда. С двумя оставшимися случаями всё короче и проще: 2) Степенной ряд сходится абсолютно при любом значении 3) Степенной ряд сходится в единственной точке. Если ряд имеет вид Других вариантов нет. Область сходимости степенного ряда – это всегда либо единственная точка, либо любое «икс», либо интервал
Поиск по сайту: |
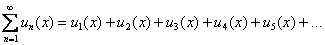
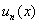 помимо многочленов, факториалов и других подарков непременновходит буковка «икс».
помимо многочленов, факториалов и других подарков непременновходит буковка «икс». . Упрощенно степенной ряд во многих учебниках записывают так:
. Упрощенно степенной ряд во многих учебниках записывают так:  , где
, где  – это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:
– это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример: 
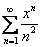 .
. то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд
то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной ряд  . Иными словами, если мы выбираем любое значение «икс» из интервала
. Иными словами, если мы выбираем любое значение «икс» из интервала 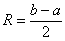

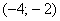 , радиус сходимости ряда:
, радиус сходимости ряда: 

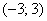 , радиус сходимости ряда:
, радиус сходимости ряда: 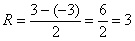
 ,
, 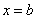 степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда: или
или 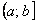 .
.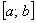
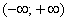 . Радиус сходимости:
. Радиус сходимости: 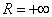 . Рисунок приводить не буду, думаю, нет необходимости.
. Рисунок приводить не буду, думаю, нет необходимости. . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:
. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:  , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке 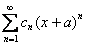 , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:
, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой: 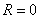 .
.