 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Когда применяется признак Даламбера?
1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, 2) В общий член ряда входит факториал. Что такое факториал? Ничего сложного, факториал – это просто свёрнутая запись произведения:
3)Если в общем члене ряда есть «цепочка множителей», например, Признак Даламбера: Рассмотрим положительный числовой ряд Исследовать ряд на сходимость Используем признак Даламбера: 4) признаки Коши; a) Радикальный признак Коши Радикальный признак Коши: Рассмотрим положительный числовой ряд Когда нужно использовать радикальный признак Коши? Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень Исследовать ряд на сходимость Мы видим, что общий член ряда полностью находится под степенью, зависящей от b) Интегральный признак Коши Интегральный признак Коши: Рассмотрим положительный числовой ряд Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом. Основной предпосылкой использования интегрального признака Кошиявляется тот факт, что в общем члене ряда есть некоторая функция и её производная.
Исследовать ряд на сходимость Как использовать интегральный признак? Сначала берем значок интеграла и переписываем со «счётчика» ряда верхний и нижний пределы: Теперь нужно вычислить несобственный интеграл 1) Если выяснится, что интеграл 2) Если выяснится, что интеграл Используем интегральный признак:
Подынтегральная функция непрерывна на
Таким образом, исследуемый ряд расходится вместе с соответствующим несобственным интегралом.
Поиск по сайту: |
 ,
,  ,
,  и так далее.
и так далее.






 .
. . Если существует предел отношения последующего члена к предыдущему:
. Если существует предел отношения последующего члена к предыдущему:  , то:
, то: ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при  .
. ряд расходится. В частности, ряд расходится при
ряд расходится. В частности, ряд расходится при  .
. признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
 , а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.
, а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.
 , то:
, то: «хорошо» извлекается из общего члена ряда.
«хорошо» извлекается из общего члена ряда.
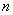 , а значит, нужно использовать радикальный признак Коши:
, а значит, нужно использовать радикальный признак Коши:

 . Затем под интегралом переписываем «начинку» ряда с буковкой «хэ»:
. Затем под интегралом переписываем «начинку» ряда с буковкой «хэ»:  . Чего-то не хватает…, ах, да, еще в числителе нужно прилепить значок дифференциала:
. Чего-то не хватает…, ах, да, еще в числителе нужно прилепить значок дифференциала:  .
.

