 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Когда применяется предельный признак сравнения?Стр 1 из 4Следующая ⇒
Ряды Числовые ряды В общем виде положительный числовой ряд можно записать так: Исследование ряда на сходимость: 1) Ряд 2) Ряд Существует несколько признаков сходимости ряда: 1) необходимый признак сходимости ряда; Если общий член рядане стремится к нулю, то ряд расходится Или короче: Если Докажем, что ряд из первого примера Ряды следующего типа:
Данный ряд называется гармоническим рядом. Легко заметить, что Также следует запомнить понятие обобщенного гармонического ряда: a) Данный ряд расходится при b) Данный ряд сходится при
2) признаки сравнения; Существуют два признака сравнения: a) признак сравнения Признак сравнения:Рассмотрим два положительных числовых ряда Иными словами: Из сходимости ряда с большими членами следует сходимость ряда с меньшими членами. Исследовать ряд на сходимость Сравним исследуемый ряд со сходящимся рядом
b) предельный признак сравнения Предельный признак сравнения:Рассмотрим два положительных числовых ряда Важные примечания: 1) Если речь идёт о двух сходящихся рядах, то предел может быть равен и нулю (но не бесконечности). 2) Если речь идёт о двух расходящихся рядах, то предел может быть равен и бесконечности (но не нулю). Когда применяется предельный признак сравнения? 1) В знаменателе находится многочлен. Исследовать ряд на сходимость Сравним данный ряд со сходящимся рядом
3) признак Даламбера;
Поиск по сайту: |
 .
. – математический значок суммы;
– математический значок суммы; – общий член ряда (запомните этот простой термин);
– общий член ряда (запомните этот простой термин);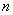 – переменная «счётчик».
– переменная «счётчик». расходится. Это значит, что бесконечная сумма равна бесконечности:
расходится. Это значит, что бесконечная сумма равна бесконечности:  .
. :
:  .
. , то ряд расходится.
, то ряд расходится. расходится.
расходится.
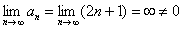
 или
или  или
или  или
или  когда в числителе и знаменателе находятся многочлены, и старшая степень числителя больше либо равна старшей степени знаменателя.
когда в числителе и знаменателе находятся многочлены, и старшая степень числителя больше либо равна старшей степени знаменателя.
 , НО. В теории математического анализа доказано, что гармонический ряд расходится.
, НО. В теории математического анализа доказано, что гармонический ряд расходится.
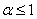 .
. .
.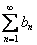 . Если известно, что ряд
. Если известно, что ряд  (для
(для 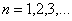 ), то ряд
), то ряд 
 . Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство
. Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство  , значит, по признаку сравнения исследуемый ряд сходится вместе с рядом
, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом  :
:  , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.
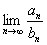 равен конечному, отличному от нуля числу, то будет доказано, что ряд
равен конечному, отличному от нуля числу, то будет доказано, что ряд  – тоже сходится.
– тоже сходится.