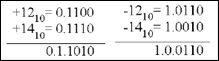Що таке суматор? Опишіть принцип дії суматора використовуючи поняття про доповняльний код

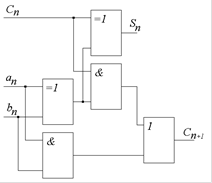
Суматор будь-якого n-го розряду, старшого за нульовий, повинен мати не два входи, а три та додавати не тільки введені в нього числа a_n і b_n, але й число С_n, яке переноситься з попереднього розряду. Схема повного суматора, який реалізує цю операцію, складається з двох напівсуматорів та одного диз’юнктора.

Для додавання багаторозрядних двійкових чисел подібні одно розрядні суматори сполучають послідовно, а результати додавання з виходів S₀-S_n та виходу переповнення С_n+1 виводять на паралельну шину. Складнішою є операція віднімання. Можна було б, звичайно, створити спеціальний пристрій для виконання цієї операції, але це означало б, що в арифметичних пристроях ЕОМ, окрім суматорів, були б присутні ще й “відніматори”, що ускладнило б їхню конструкцію. Виявилося, що простіше використовувати для операції віднімання ті ж суматори, розглядаючи віднімання як додавання додатних та від’ємних чисел, а останні подавати у доповняльному коді. Для здійснення операції додавання/віднімання з n-розрядними числами використовують (n+1)-розрядний повний суматор, до якого додається пристрій для перетворення числа у доповняльний код .

Сигнал із знакового розряду числа подається на вхід С₀ та а_n+1, а всі значущі розряди n-розрядного двійкового числа інвертуються або не інвертуються за допомогою n елементів нерівнозначності, якими керує знаковий сигнал. Через вхід С₀ до наймолодшого розряду додається або не додається одиниця. Аналогічною схемою слід спорядити також всі входи для операнда “b”. Справа ускладнюється тим, що в ряді випадків може трапитися переповнення значущих розрядів і перехід одиниці в надстарший S_n+1 розряд суматора, де належить бути символу знаку, адже на всіх n виходах суматора S_n числа будуть подані у доповняльному коді. Так виходить, наприклад, коли додавати числа +12 та +14. Більше того, на прикладі додавання чисел -12 та -14, видно, що може переповнитись і знаковий розряд, а одиниця перейде до С_n+1.

Аналіз можливих комбінацій S_n+1 та C_n+1 показує, що якщо S_n+1=C_n+1, то справжнього переповнення суматора не відбувається, і отже, нехтуючи виходом одиниці за межі суматора, можна розглядати число на S-виходах як результат додавання, зображений у доповняльному коді. Якщо ж S_n+1≠C_n+1, суматор переповнений, в знаковому розряді опиниться надстарший розряд значущого числа, а знак опиниться на виході C_n+1. Такий результат буде помилковим і про це треба повідомити. Реалізація цих міркувань здійснюється за допомогою елемента нерівнозначності, підключеного до S_n+1 та C_n+1 виходів суматора. На виході цього елемента сигнал високого рівня з’явиться при Sn+1≠Cn+1, що буде сигналізувати про помилку у результаті. Комбінуючи операції додавання і віднімання зі зсувом праворуч чи ліворуч можна також виконувати операції множення та ділення.

Поиск по сайту: