 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Динамика систем обратной связи
В предыдущем параграфе мы пренебрегали тем обстоятельством, что простейшие управляемые объекты осуществляют функции усиления сигнала не мгновенно, а с некоторым запаздыванием. Практически в природе нет таких объектов, которые бы реагировали на управляющий сигнал мгновенно. На рисунке 4.2 даны типичные зависимости усиленных сигналов xвых при скачкообразном включении входного сигнала xвх. Запаздывание реакции исполнительного органа на сигнал управления приводит к тому, что в системах с отрицательной обратной связью (рисунок 4.1) возникают побочные явления, нарушающие устойчивость. В неравновесной термодинамике они именуются детерминированным хаосом. Лучше всего это понять на примере двух встречных пешеходов, случайно столкнувшихся на тротуаре и пытающихся разойтись. Пешеход, идущий с одной стороны, делает шаг вправо, пытаясь обойти случайно оказавшегося перед ним господина. Но тот, в силу замедленности реакции делает то же самое, т.е. шаг влево. Ситуация противостояния сохраняется. Теперь первый пешеход двигается влево. Его визави, поняв свою ошибку, тоже возвращается на прежнююколею. Они вновь остаются друг против друга. Колебательные движения прекращаются
Рисунок 4.2. Типичные зависимости выходных сигналов от времени: а- чистое запаздывание; б- экспоненциальное нарастание; в- гармоническая зависимость
только тогда, когда один из бедолаг изменит тактику – перестанет прыгать и остановится, или прыгнет в другую сторону, или (наихудший вариант) толкнет ни в чем не повинного случайного партнера. Ясно, что если бы реакция каждого пешехода, или хотя бы одного из них была моментальной, эта жуткая сцена не возникла. То же самое возникает в природе, но с той разницей, что нет контролирующего органа, который бы прекратил бессмысленные блуждания. Незатухающие автоколебания в системах обратной связи возникают при вполне определенных соотношениях между параметрами, характеризующими инерционность отдельных органов этих систем, и их коэффициентами усиления. Системы с незатухающими, особенно нарастающими автоколебаниями достаточно быстро разрушаются*. В любом случае реализация передачи информации от эталонного к исполнительному органу сопровождается некоторым запаздыванием, в течение которого процесс протекает достаточно хаотично. В теории автоматического управления описываются различные способы устранения этого хаоса и ускорение процесса окончательной передачи информации от источника эталонного (управляющего) сигнала к управляемому объекту. Наиболее эффективный способ – так называемая гибкая обратная связь. Суть ее сводится к тому, что параллельно общей цепочке – “измерительный орган (датчик) – орган сравнения – усилительный орган " – подключается орган гибкой обратной связи, сигнал на выходе которого пропорционален производной Рио (рисунок 4.1):
В этом случае выходной сигнал исполнительного органа равен:
Наличие дополнительного слагаемого, возникающего только при изменении Рио, т.е. при переходном процессе, позволяет ускорить наступление стационарного режима.Коэффициент Кг.о.с. может быть отрицательным. В этом случае процесс установления замедляется, зато протекает плавно, без сильных выплесков Рио в переходный период.
4.4. Непрерывные (аналоговые) и дискретные (цифровые) способы передачи информации в управляемых системах Как указывалось в §3.5, передача информации в природе осуществляется только дискретно, с помощью конечных порций, и может рассматриваться нами как непрерывная только в силу малости отношения каждой такой порции ко всей информации. В качестве примера приведем речь. Когда один что-то говорит другому, тому представляется, что информация поступает непрерывно. Однако весьма неглубокий анализ такой ситуации легко опровергает такое восприятие. Действительно, почему мы можем записать все, что нам говорят? Потому что речь состоит из предложений (фраз), слов, а эти последние – из звуков: по сути дела, элементарных порций речевой информации. Именно эти звуки мы можем перевести в буквы и записать соответствующий текст. Приведем еще насколько примеров передачи информации (и ее получения) в дискретной форме. Вот, например, как воспринимают зрительную информацию наши глаза? На рис. 6.3 изображена оптическая система глаза. Как видим, его чувствительным органом служит сетчатка, расположенная в глазном дне. Она состоит из расположенных в виде решетки окончаний нервных волокон, которые отправляют полученное световое раздражение в головной мозг. Следовательно, мы видим окружающий мир в виде мозаики, ячейки которой, правда, настолько малы, что он представляется нашему мозгу сплошным (непрерывным). Кинофильм представляет собой череду быстро (со скоростью 24 кадра в секунду) сменяющих друг друга фотокартинок, каждая из которых отличается от предыдущей небольшим, но все-таки конечным, изменением размера изображаемых объектов. Аналогично дискретно передается и воспроизводится видеоинформация в телевизоре. Музыкальные произведения дискретизируются с помощью нот. В настоящее время общепринята равномерно-темперированная шкала звуков, содержащая 12 полутонов в каждой гамме. Она использует особенность слуха – воспринимать изменение тональности (высоты) звука пропорционально не его частоте, а логарифму частоты. Вследствие этого два акустических колебания, отличающиеся частотой в два раза, образуют базовый звуковой диапазон – октаву. Если в качестве источника звука выбрать струнный инструмент, то получить октаву одной струны можно, уменьшив ее длину в два раза. Частота колебаний половины струны – 0,5l – в 2 раза больше частоты колебаний полной струны (нота «до»). Нота «соль» соответствует 2/3 длины струны, т.е. частоте, в 1,5 раза большей частоты колебаний всей струны. Ухом она воспринимается как
Нота «фа» соответствует 3/4 длины струны т.е.
Нота «ми» создается 4/5l :
Нота «ми бемоль» – 5/6l :
и т.д. [45]. Одним из вариантов дискретной системы обратной связи является обычный бытовой холодильник (рисунок 4.3,а). Исполнительным органом холодильника является блок "компрессор К - приводной электродвигатель". Измерительным органом - термодатчик Д. Органом сравнения и эталонным органом является терморегулятор. Усилительным органом – реле терморегулятора. Эталонный орган терморегулятора настроен так, что при температуре, на 2 - 3% большей номинальной, он включает реле, а на 2- 3 % меньшей – отключает. Работает холодильник так. При отключенном компрессоре температура внутри шкафа холодильника постепенно повышается за счет теплопроводности стенки (см. график 1 рисунок 4.3,б). После того, как температура внутри шкафа поднялась на 2 - 3% выше установленной, разность между сигналом термодатчика и эталонным сигналом становится близкой к нулю. Реле терморегулятора включается (рисунок 4.3, б), и компрессор путем прогона охлаждающей жидкости понижает температуру внутри шкафа. Когда температура снизится на 2 - 3% ниже номинальной, реле отключается. Компрессор перестает работать. Отвод тепла из камеры шкафа холодильника прекращается, и он вновь начинает медленно нагреваться. Таким образом, температура камеры пульсирует на 2 - 3 % выше и ниже номинальной (рисунок 4.3,б). Как видим, в дискретной системе роль управляющего органа проще, чем в непрерывной: от эталонного исполнительному органу передается простейшая информация да - нет. Да - это когда компрессор включается, нет - когда он отключен.Большинство природных регуляторов действует именно по этому принципу.
Схема холодильника: Ш - шкаф, З - змеевик с протекающей по нему охлаждающей жидкостью, Т - теплообменник, Р - расширитель, Д - термодатчик с терморегулятором, К - компрессор с приводным электродвигателем, Рк - мощность компрессора, Т0 - температура шкафа.
Так осуществляется открытие и закрытие клапанов в кровеносных сосудах. Именно такие сигналы передаются по нервным клеткам. Воздействие катализаторов (энзимов) обеспечивает начало и дальнейшее протекание химических реакций в клетках. Добавка всего одного кристаллика приводит к объемной кристаллизации в насыщенном растворе какой-либо соли в воде. Простейшая информация да - нет позволяет выстроить сколь угодно сложную структуру с помощью определенной цепочки последовательных передач этой информации. Более того. Можно с уверенностью сказать, что в природе нет фактически систем непрерывной передачи информации – все системы дискретные. В теории автоматического управления имеется теорема Котельникова, которая обосновывает возможность представления непрерывных функций дискретными и наоборот. Поэтому всё, что ниже будет сказано о дискретных системах накопления информации, относится ко всем без исключения объектам управления. Для описания дискретной структуры в математике разработана так называемая алгебра логики. Эта алгебра использует всего две цифры 0 и 1. Первая цифра соответствует отсутствию информации (нет), а вторая – ее наличию (да). Алгебра логики содержит следующие элементарные операции 1) сложение (дизъюнкция):
Знак дизъюнкции "V" иногда заменяют привычным "+", а также словом или: один или один = один; один или ноль = один и т.д. 2) умножение (конъюнкция):
Знак конъюнкции иногда заменяют привычными 3) отрицание (инверсия):
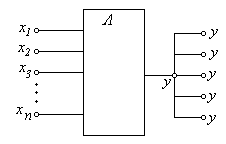
Знак инверсии заменяется словом не. В сущности, этих трех действий достаточно, чтобы составить весьма сложные системы передачи дискретной информации. Материальные объекты, осуществляющие такую передачу, именуются автоматами. В рассмотренном выше примере с холодильником автоматом является термореле. На рисунке 4.4, а, б изображены схемы дизъюнктора или автомата-сумматора [18]. Величины х1, х2, ..., хn принимают значения 0 или 1, т.е. являются логическими функциями. Выходная величина дизъюнктора (рисунок 5.4, а) равна
На рисунке 4.4, б изображена схема конъюнктора или автомата-множителя. Выходная функция рисунка 4.4, б равна:
На рисунке 4.4, в дана схема инверсора – автомата, реализующего операцию инверсии – замену входного сигнала на противоположный. На рисунке 4.4, г дана схема автомата, реализующего суммирование нескольких логических чисел, часть из которых подверглась инверсии (те, которые изображены отрезком с кружочком на правом конце):
На рисунке 4.4, д изображен еще один базовый автомат - таймер, в задачу которого входит “запоминание” поступившего сигнала на некоторый интервал времени Следует обратить внимание на то, что большинство автоматов рисунка 4.4 понижает энтропию, т.е. увеличивает порядок.Действительно, количество возможных вариантов комбинаций n чисел х1, х2, ..., хn, каждое из которых принимает значение 0 или 1 равно 2n.Например, если n=4, то всего возможно 16 комбинаций - таблица 4.1
еж Рисунок 4.4 а – дизъюнктор;б – конъюнктор; в – инверсор; г – логический автомат или-не; д – таймер; е – зависимости x(t),y(t) для таймера; ж – конъюнктор с несколькими выходами.
Таблица 4.1
Количество комбинаций на выходе простейших автоматов равно двум. Таким образом, энтропия понижается каждым автоматом на величину:
Если автомат имеет m выходов - рисунок 4.4,ж, то образуемая им информация Различные комбинации автоматов позволяют еще более увеличить степень упорядочивания системы. Строго говоря, базовых операций с логическими числами не четыре, как показано выше, а только три. Дело в том, что конъюнкцию можно представить себе как комбинацию операций дизъюнкции и инверсирования. Действительно, если все входные сигналы дизъюнктора-инверсора или –не (рисунок 4.4, г) инверсировать, то сигнал его выхода y будет равен
Если теперь инверсировать дополнительно выходной сигнал у (т.е. на выходе 4.4, г установить инверсор рисунок 5.4, в), то получим
Как видим, выходной сигнал этого комбинированного логического органа соответствует выходному сигналу элемента рисунок 4.4, б, т.е. конъюнктора. Использование инверсии в качестве дополнительного процесса обработки логической информации увеличивает ее величину. Действительно, если в дизъюнкторе (рисунок 4.4, г) число инверсных входов равно l < n, то энтропия входных сигналов будет составлять не n, а
Следовательно, получаемая в этом случае информация равна
Возможны логические элементы, в которых инверсные входы варьируются не только местами, но и числом (т.е. l = 0÷n). В этом случае l
Как видим, хотя операция инверсии сама по себе дополнительной информации не дает, зато в комбинации с дизъюнкцией существенно увеличивает возможность повышения порядка.
Поиск по сайту: |

 (4.12,а)
(4.12,а) (4.12,б)
(4.12,б) [бит].
[бит]. [бит].
[бит]. [бит].
[бит]. [бит].
[бит].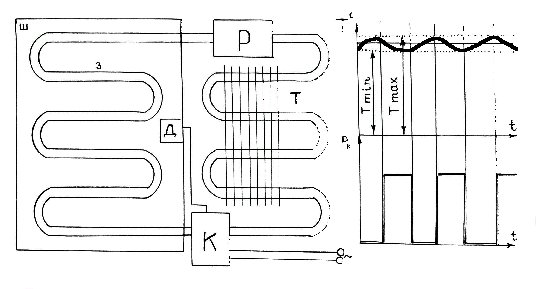
 (4.14)
(4.14)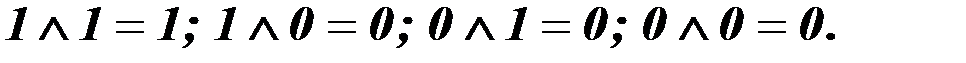 (4.15)
(4.15) или х, а также междометием и: один и один = один; один и ноль = ноль и т.д.
или х, а также междометием и: один и один = один; один и ноль = ноль и т.д. (4.16)
(4.16) =
=  .
.

 . Это значит, что сигнал на выходе таймера возникнет спустя
. Это значит, что сигнал на выходе таймера возникнет спустя  секунд и будет соответствовать сигналу х (рисунок 4.4,е).
секунд и будет соответствовать сигналу х (рисунок 4.4,е). в
в
 а
а
 б
б
 г
г
 д
д


 I = (n - 1)m.
I = (n - 1)m.
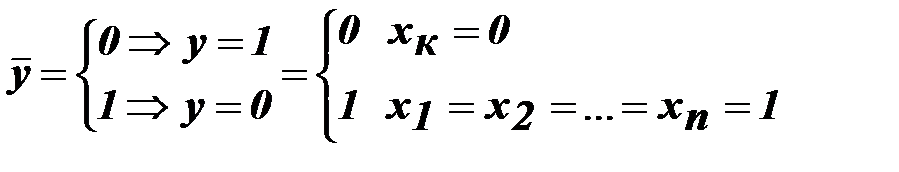
 бит, где
бит, где 
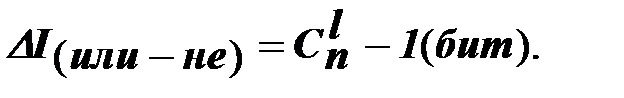 (4.17)
(4.17) (4.18)
(4.18)