 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема Гаусса для электростатики (в интегральной и дифференциальной форме)
Поток вектора напряженности электрического поля.Пусть небольшую площадку ΔS пересекают силовые линии электрического поля, направление которых составляет с нормалью nк этой площадке угол α.
Полагая, что вектор напряженности Ене меняется в пределах площадки ΔS, определим поток вектора напряженности через площадку ΔS как ΔФE = E ΔS cos α. (1) Поскольку густота силовых линий равна численному значению напряжённости E, то количество силовых линий, пересекающих площадку ΔS, будет численно равно значению потока ΔФE через поверхность ΔS. Для элементарной площадки dS выражение (1) принимает вид dФE = E dS Через всю площадку S поток вектора напряженности вычисляется как интеграл по поверхности Теорема Гаусса.Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхности S. Поток вектора индукции через элемент поверхности dS равен Если электрическое поле создаётся системой точечных зарядов q1, q2,…, qn, которая охватывается замкнутой поверхностью S, то, в соответствии с принципом суперпозиции, поток вектора индукции через эту поверхность определяется как сумма потоков, создаваемых каждым из зарядов. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:
Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём dV имеет заряд
Выражение (4) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности. Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Дифференциальная форма теоремы Гаусса.Отметим, чтоинтегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема V на малые объемы Vi , получим выражение справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом: и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D): Дивергенция вектора Dв декартовых координатах: Таким образом выражение (5) преобразуется к виду: Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора Dсвязана с плотностью заряда в той же точке равенством
или для вектора напряженности электростатического поля
Эти равенства выражают теорему Гаусса в дифференциальной форме. Отметим, что в процессе перехода к дифференциальной форме теоремы Гаусса получается соотношение, которое имеет общий характер: Выражение называется формулой Гаусса - Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем. Вопрос №5. Потенциальный характер электростатического поля. Интегральная и дифференциальная формулировки критерия потенциальности. Скалярный потенциал, разность потенциалов. Градиент потенциала. Уравнения Пуассона и Лапласа. Поле сил называется потенциальным, если работа при перемещении заряда в этом поле зависит лишь от начальной и конечной точек пути и не зависит от траектории (а также А=0 при перемещении по замкнутому контуру). Кулоновская сила убывает обратно пропорционально квадрату расстояний (как и сила тяжести точечной массы, которая является потенциальной), следовательно, она является потенциальной. Из потенциальности поля точечного заряда => потенциальность произвольного электрического поля (по суперпозиции).
Вопрос №6.
Поиск по сайту: |
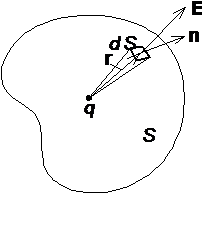

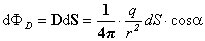 (2)
(2)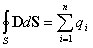 (3)
(3)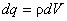 . В этом случае в правой части выражения (3) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:
. В этом случае в правой части выражения (3) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S: (4)
(4)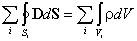
 (5)
(5)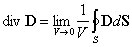

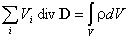 .
.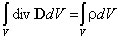
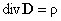
 .
.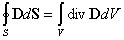 .
.


