|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Комбинированные задания по разделу
«Квадратные корни» = 10
Уровень1
1. Упростите выражение а) 0; б) 2.Верно ли , что а) 5; б) –5; в) 4; г) 0 ?
3.Упростите выражение ( а) 6; б) –6; в) 1; г) 5.
Выберите правильные ответы
Ответы 1.а); 2. а) , в) г) 0; 3. г) .
Уровень 2
1. Упростите выражение а) 6; б) –6; в) 1; г) 5.
2.Верно ли, что
а) х = 0; б) х = 7; в) х = -7; г) -2?
3.Результат упрощения выражения а) 6; б)
Выберите правильные ответы
Ответы 1.а); 2. а) , в) г) 0; 3. г) .
Уровень 3
1. Результат умножения выражения
а) 11; б) 5; в) – 5 г)
2. Вычислите а) -5,2; б) 7 ; в) 7,6 ; г)
3. Верно ли, что а) х = 1,2; б) х = 4; в) х = - 4 г) х =
Выберите правильные ответы
Ответы 1.б); 2. в); 3.а) , б), г) .
Уровень 4
1. Если а) 0,4; б) 5,2; в) - 4; г) 2,5
2. Упростите выражение а) |x|; б) х; в) 3х - 2; г) |х| -1.
3. Какие из значений х входят в облаcть определения функции y = а) x=0,09; б) x=
Выберите правильные ответы
Ответы 1.г); 2. а); 3.а) , в), г) .
Уровень5
1. Результат упрощения выражения а)
2.Результат упрощения выражения
а)
3. Освободитесь от иррациональности в знаменателе
а) в)
Выберите правильные ответы
Ответы 1.а); 2. г); 3.а).
Дополнительно Рациональной дробью называется упорядоченная пара целых чисел (m, n), где n¹0, обозначаемая символом
Две рациональные дроби Свойства отношения эквивалентности: 1) рефлекcивность (любая рациональная дробь эквивалентна самой себе): 2) симметричность: 3) транзитивность: Из определения эквивалентных дробей следует основное свойство дроби: если числитель и знаменатель дроби Переход от дроби Свойство эквивалентности рациональных дробей позволяет дать несколько иное определение рациональной дроби: рациональной дробью называют пару чисел (m, n), обозначаемую символом Если m > 0, то рациональная дробь называется положительной, если m < 0 – отрицательной, её записывают в виде Рациональным числом называется множество всех эквивалентных между собой рациональных дробей. Множество рациональных чисел обозначается Q. В соответствии с определением рационального числа, различные эквивалентные между собой дроби – это лишь различные записи одного и того же рационального числа. Рациональное число называется целым, если во множестве соответствующих ему эквивалентных дробей содержится дробь вида Суммой двух рациональных чисел Можно доказать, что сложение рациональных чисел а) с одинаковыми знаменателями выполняется по правилу б) с разными знаменателями выполняется по правилу Разностью рациональных чисел Можно доказать, что разность двух рациональных чисел Произведением двух целых чисел Частным рациональных чисел а) частное двух рациональных чисел б) Числитель положительной неправильной дроби можно представить в виде Система аксиом действительных чисел: 1. Свойство упорядоченности: для любых двух чисел определено отношение порядка, т.е. для любых двух чисел a и b либо a = b, либо a > b, либо a < b. 2. Свойства операции сложения: для любых двух чисел определена операция сложения, т.е. любой упорядоченной паре чисел a и b ставится в соответствие единственное число, называемое их суммой и обозначаемое a + b, при этом 1) для любой пары чисел a и b выполняется равенство a + b = a + b (коммутативность сложения); 2) для любой тройки чисел a, b, с выполняется равенство (a + b) +с = a + (b +c) (ассоциативность сложения); 3) существует число, обозначаемое символом 0 и называемое нулём, такое, что для любого числа a выполняется равенство a + 0 = a; 4) для любого числа a существует число, обозначаемое (–a) и называемое противоположным числу a, такое, что a + (– a) = 0; 5) если a < b, то для любого числа c выполняется неравенство a+c < b+c. Для любой упорядоченной пары чисел a и b число a + (–b) называется разностью чисел и обозначается a – b. 3. Свойства операции умножения: для любых двух чисел определена операция умножения, т.е. любой упорядоченной паре чисел a и b ставится в соответствие единственное число, называемое их произведением и обозначаемое a × b, при этом 1) для любой пары чисел a и b выполняется равенство a × b = a × b (коммутативность умножения); 2) для любой тройки чисел a, b, с выполняется равенство (a × b) ×с = a × (b ×c) (ассоциативность умножения); 3) существует число, обозначаемое символом 1 и называемое единицей, такое, что для любого числа a выполняется равенство a ×1 = a; 4) для любого числа a, отличного от 0 существует число, обозначаемое 5) если a < b и с > 0, то a×c < b×c, если a < b и с < 0, то a×c > b×c. Для любой упорядоченной пары чисел a и b (b¹0) число 4. Связь операций сложения и умножения: (a + b) × c = a×c + b×c (дистрибутивность умножения относительно сложения). 5. Свойство Архимеда: для любого числа a существует такое целое число n, что n £ a < n+1. 6. Свойство непрерывности (это свойство не характерно для множества рациональных чисел, существует несколько различных его формулировок, одна из них называется принципом вложенных отрезков или аксиомой непрерывности по Кантору). Если заданы два числа a и b, a £ b, то множество всех чисел x, таких, что Принцип вложенных отрезков: для всякой системы вложенных отрезков существует хотя бы одно число, которое принадлежит всем отрезкам данной системы. Из этого принципа следует, что для всякой системы вложенных отрезков, по длине стремящихся к 0, существует единственное число, принадлежащее всем отрезкам данной системы.
Поиск по сайту: |
 ;
; ; в) -
; в) - 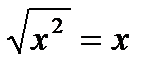 при х, равным
при х, равным .
. ;
; , если
, если равен
равен ; в) 1; г)
; в) 1; г) 
 на сопряженное ему равен
на сопряженное ему равен

 .
. , если
, если , то значение выражения
, то значение выражения 

 -3; в) x =
-3; в) x = 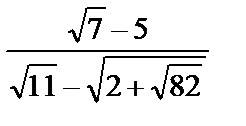 ; г) 8-2
; г) 8-2  ?
? равен
равен б)
б)  ; в) 3; г) 6.
; в) 3; г) 6. при a < -2 равен
при a < -2 равен б)
б)  в) -1; г) 1.
в) -1; г) 1. .
. ;б)
;б) 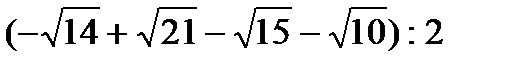 ;
; ; г)
; г)  ;
; равно
равно
 ;2)0
2) 1; 3) 6 ; 5)
;2)0
2) 1; 3) 6 ; 5)
 равен
равен


 ; 2)22;
3)-22; 4) -4
; 2)22;
3)-22; 4) -4  ; 5)0.
; 5)0.

 равно
равно
 -20 ; 2)20;
3)-40; 4) -4
-20 ; 2)20;
3)-40; 4) -4  ; 5)0.
; 5)0.
 равно
равно
 ;2)0;
3)
;2)0;
3)  ; 4)2
; 4)2  ;
5)-
;
5)- 
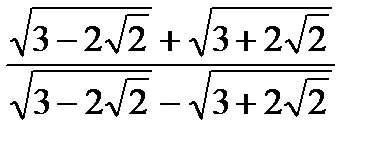 равно
равно
 ;2)0;
3)
;2)0;
3)  ; 4)2
; 4)2 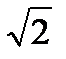 ;
5)
;
5) 
 равно
равно
 ; 4)-
; 4)-  ;
5)
;
5) 
 , то значение выражения
, то значение выражения  равно
равно
 равен
равен
 равен
равен
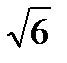 ;
5)
;
5)  равно
равно
 ;2)0;
3)
;2)0;
3)  ; 4)5
; 4)5  равен
равен
 ; 2)14;
3)4; 4) -4; 5)0.
; 2)14;
3)4; 4) -4; 5)0.
 равен
равен
 ;2)0;
3)
;2)0;
3) 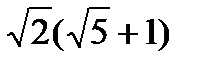 ; 4)
; 4)  равен
равен
 ; 5)0.
; 5)0.
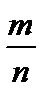 . Число m называется числителем дроби, число n – знаменателем дроби.
. Число m называется числителем дроби, число n – знаменателем дроби.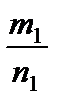 и
и  называют эквивалентными, если
называют эквивалентными, если  . Записывают:
. Записывают:  ~
~  .
. ~
~  ;
; ~
~  Þ
Þ  ~
~  ;
; ~
~  и
и  ~
~  Þ
Þ  ~
~ 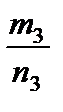 .
. умножить на одно и то же целое число k ¹ 0, то получится дробь
умножить на одно и то же целое число k ¹ 0, то получится дробь  , эквивалентная дроби
, эквивалентная дроби 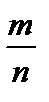 .
. к эквивалентной дроби
к эквивалентной дроби 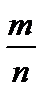 называют сокращением дроби на число k. Дробь называется несократимой, если её числитель и знаменатель – взаимно простые числа.
называют сокращением дроби на число k. Дробь называется несократимой, если её числитель и знаменатель – взаимно простые числа. , где m – целое число, n – натуральное число.
, где m – целое число, n – натуральное число. . Положительная рациональная дробь
. Положительная рациональная дробь  называется правильной , если m < n; и неправильной, если m ³ n.
называется правильной , если m < n; и неправильной, если m ³ n. . Равенство двух рациональных чисел понимается как совпадение соответствующих им множеств эквивалентных рациональных дробей.
. Равенство двух рациональных чисел понимается как совпадение соответствующих им множеств эквивалентных рациональных дробей. и
и  называется число
называется число  .
. +
+  =
=  .
. +
+  =
= 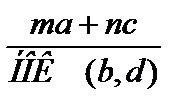 , где
, где 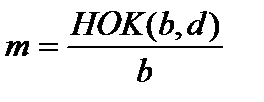 ,
, 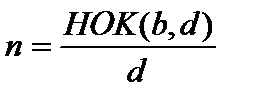 .
. и
и  называется рациональное число
называется рациональное число  такое, что
такое, что  .
. .
.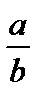 и
и  называется число
называется число  .
. называется рациональное число
называется рациональное число  . Можно доказать, что
. Можно доказать, что ;
;
 , где
, где  ,
,  , r< n, тогда дробь запишется в виде
, r< n, тогда дробь запишется в виде  . Число k называется целой частью дроби. Если r ¹0, то дробь
. Число k называется целой частью дроби. Если r ¹0, то дробь  записывают в виде смешанной дроби
записывают в виде смешанной дроби  .
. и называемое обратным числу a, такое, что
и называемое обратным числу a, такое, что  .
. называется частным от деления a на b и обозначается
называется частным от деления a на b и обозначается  .
. называется числовым отрезком и обозначается
называется числовым отрезком и обозначается  . Число b – a называется длиной числового отрезка. Система числовых отрезков
. Число b – a называется длиной числового отрезка. Система числовых отрезков  ,
,  ,…,
,…,  называется системой вложенных отрезков, если
называется системой вложенных отрезков, если