 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Истечение сжимаемого газа
При истечении газа (пара, воздуха) в окружающую среду под высоким давлением резко изменяется его объем. Поэтому необходимо учитывать сжимаемость газа. Исследуем адиабатическое истечение идеального газа из резервуара (пренебрегая потерями в насадке), где он находился под давлением ро, в среду с давлением р. Применяя к сечениям струйки газа в резервуаре, где скорость близка к нулю, а в сжатом сечении уравнение энергии в форме (11), будем иметь:
откуда
Выражая r0/r через p/p0 с помощью уравнения адиабаты (4) и используя уравнение состояния (3), получим формулу Сен-Венана и Венцеля для скорости адиабатного истечения газа:
С уменьшением p/p0 скорость истечения u возрастает до тех пор, пока не достигнет критического значения. Критической называется скорость течения, равная местной скорости звука. Величину критической скорости легко определить из уравнения энергии в форме (14) или (15), если принять u = a = aкр:
при это критическое отношение давлений равно:
В частности, для воздуха, при температуру 15°C, aкр = 0,91a0 = 310 м/с. При дальнейшем уменьшении внешнего давления p скорость истечения остается неизменной и равной αкр . Теоретический массовый расход MТ газа при истечении из отверстия с учетом потерь в насадке для случая, когда p/p0 ³ (p/p0)кр , равен:
При p/p0 < (p/p0)кр выражение для MТ имеет вид
Массовый расход в этом случае от внешнего давления p не зависит, а определяется давлением p0 в резервуаре, возрастая с его увеличением. При экспериментальном исследовании истечения газов из сужающегося сопла было обнаружено, что невозможно получить давление газа в выходном сечении сопла ниже некоторого критического давления. Этому критическому давлению соответствует максимальный расход газа через сопло. Отношение критического давления к начальному давлению на входе в сопло может быть определено по формуле
Это означает, что критическое отношение давлений газов зависит только от рода газа и для конкретного газа является постоянным. Для двух атомных газов и воздуха
где Постоянный критический перепад давлений объясняется характером распространения возмущений в среде. Известно, что любое слабое возмущение, в том числе и изменение давления, распространяется в сжимаемой среде со звуковой скоростью, а скорость истечения через сужающееся сопло при т. е. при В действительности процессы истечения через сопла и отверстия всегда неравновесные, необратимые. Они сопровождаются потерями работоспособности и увеличением энтропии и энтальпии газа и поэтому и действительная скорость - коэффициент скорости сопла - коэффициент истечения(коэффициент расхода сопла) Значения этих коэффициентов находится опытным путем, и в этом состоит одна из целей работы. Обычно с увеличением скорости
Поиск по сайту: |
 ,
, .
. . (22)
. (22) , (23)
, (23) . (24)
. (24) . (25)
. (25)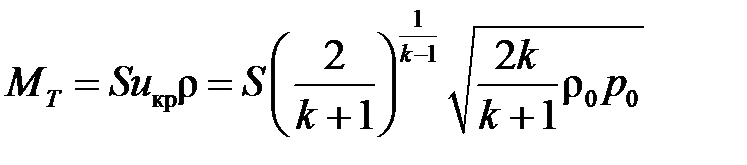 . (26)
. (26) . (27)
. (27) и
и 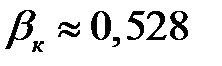 . Для одноатомных газов
. Для одноатомных газов  ,
,  . Для трех- и многоатомных газов
. Для трех- и многоатомных газов  ,
,  . Если давление среды за соплом понижать до давлений, меньших
. Если давление среды за соплом понижать до давлений, меньших 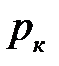 ,то это не повлияет на давление газа на срезе сужающегося сопла
,то это не повлияет на давление газа на срезе сужающегося сопла  . Оно будет оставаться постоянным и
. Оно будет оставаться постоянным и  , а скорость истечения из сужающегося сопла при
, а скорость истечения из сужающегося сопла при  будет также оставаться постоянной и равной местной скорости звука
будет также оставаться постоянной и равной местной скорости звука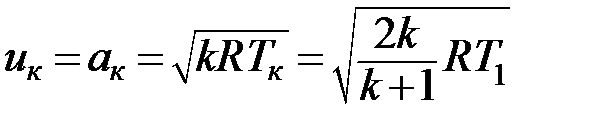 . (28)
. (28) − температура на выходе из суживающегося сопла (в «критическом» сечении).
− температура на выходе из суживающегося сопла (в «критическом» сечении). ниже
ниже  возмущение среды не проникает внутрь сопла, т. к. его относительная скорость будет равна нулю,
возмущение среды не проникает внутрь сопла, т. к. его относительная скорость будет равна нулю,  .
.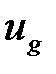 , и действительный расход газа
, и действительный расход газа  всегда несколько ниже, чем теоретические:
всегда несколько ниже, чем теоретические:  ,
,  . В расчетах это учитывают введением соответствующих коэффициентов
. В расчетах это учитывают введением соответствующих коэффициентов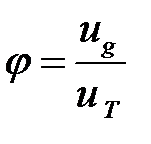 ;
; .
. величины коэффициентов увеличиваются, а их численные значения существенно зависят от ряда факторов, в том числе от качества обработки поверхности канала, его формы и геометрических размеров.
величины коэффициентов увеличиваются, а их численные значения существенно зависят от ряда факторов, в том числе от качества обработки поверхности канала, его формы и геометрических размеров.